1900-ാമാണ്ടിൽ ക്വാണ്ടം എന്ന ആശയം ആദ്യമായി അവതരിപ്പിച്ചത് മാക്സ് പ്ലാങ്കാണ് (Max Planck, 1858-1947). അദ്ദേഹത്തിൻ്റെ സിദ്ധാന്തത്തെക്കുറിച്ചു പറയുന്നതിനു മുമ്പ് ആദ്യം കുറച്ചു ചരിത്രം മനസ്സിലാക്കിയാൽ കാര്യങ്ങൾ എളുപ്പമാകും. നമുക്ക് 19-ാം നൂറ്റാണ്ടിലെ യൂറോപ്പിലേക്ക് ഒന്നു പോകാം. അവിടെ വ്യാവസായിക വിപ്ലവം നടക്കുന്ന കാലമാണത്. കൽക്കരി ഉപയോഗിച്ചു പ്രവർത്തിക്കുന്ന ആവി എഞ്ചിനുകളാണ് അതിനു വേണ്ട ഊർജം നൽകിയിരുന്നത്. ആദ്യകാല ആവി എഞ്ചിനുകളുടെ എഫിഷ്യൻസി വളരെ കുറവായിരുന്നു. താപോർജത്തിൻ്റെ എത്ര ഭാഗം മെക്കാനിക്കൽ എനർജിയാക്കി മാറ്റാൻ എഞ്ചിനുകൾക്ക് കഴിയുന്നു എന്നതാണ് എഫിഷ്യൻസി എന്ന വാക്കുകൊണ്ടു സൂചിപ്പിക്കുന്നത്. അതു കൂട്ടാനുള്ള ശ്രമം തെർമോഡൈനാക്സിൻ്റെ ആഴത്തിലുള്ള പഠനത്തിനു പ്രചോദനമായി. 19-ാം നൂറ്റാണ്ടിൻ്റെ ഒടുക്കമാകുമ്പോഴേക്കും വൈദ്യുതി വിളക്കുകളും രംഗത്തെത്തുന്നു. ഫിലമെൻ്റു ബൾബുകൾ വെളിച്ചം വിതറാൻ തുടങ്ങിയപ്പോൾ അതിൻ്റെ താപനിലയും പുറത്തുവിടുന്ന പ്രകാശവും തമ്മിലുള്ള ബന്ധം പഠിക്കാനും ഡിമാൻഡുണ്ടായിരുന്നു.
മാക്സ് പ്ലാങ്ക് ജോലി ചെയ്തിരുന്നത് ജർമ്മനിയിൽ ബർലിനിൽ ആയിരുന്നു. അവിടെ അദ്ദേഹത്തിൻ്റെ ഗുരുവായിരുന്ന ഗുസ്താഫ് കിർച്ചോഫിൻ്റെ (Gustav Kirchhoff) പിന്തുടർച്ചക്കാരനായി ജോലിയിൽ പ്രവേശിച്ച പ്ലാങ്ക് ബ്ലാക്ക് ബോഡി താപ വികിരണത്തെക്കുറിച്ച് ആഴത്തിൽ പഠിക്കാൻ തുടങ്ങി. കിർച്ചോഫ് ആണ് ബ്ലാക്ക് ബോഡിയെന്ന ആശയം ദശാബ്ദങ്ങൾക്കു മുമ്പേ ആദ്യമായി അവതരിപ്പിക്കുകയും പഠിക്കുകയുംചെയ്ത ശാസ്ത്രജ്ഞൻ. കിർച്ചോഫ് കണ്ടത്തിയ ഒരു കാര്യം പ്രകാശത്തെ, അല്ലെങ്കിൽ താപവികിരണത്തെ ആഗിരണം ചെയ്യുന്ന ഏതൊരു വസ്തുവും അതേ തരം വികിരണത്തെ പുറത്തുവിടുകയും ചെയ്യും എന്നതാണ്.
ഇതു കുറച്ചുകൂടി വ്യക്തമാക്കാൻ ഒന്നു ശ്രമിക്കാം. കിർച്ചോഫിൻ്റെ ഈ നിയമം ബാധകമായിട്ടുള്ളത് താപസന്തുലനാവസ്ഥയിൽ (thermal equilibrium) ഉള്ള വസ്തുക്കൾക്കാണ്. താപസന്തുലനാവസ്ഥ എന്നു വെച്ചാൽ താപനില (temperature) കൂടുകയോ കുറയുകയോ ചെയ്യാതെ ഒരേ നിലയിൽ തന്നെ തുടരുന്ന അവസ്ഥ. എന്നുവെച്ചാൽ ചുറ്റുപാടിൽ നിന്ന് കൊടുക്കൽ വാങ്ങലുകൾ ഇല്ലാതെ ഒറ്റപ്പെട്ടിരിക്കുന്ന അവസ്ഥ എന്ന് അർത്ഥമില്ല. പുറത്തേക്കു കൊടുക്കുന്ന അത്രതന്നെ താപോർജം അതു സ്വീകരിച്ചു കൊണ്ടും ഒരു വസ്തുവിന് സന്തുലനാവസ്ഥ നിലനിർത്താം.
2.1 കിർച്ചോഫിന്റെ റേഡിയേഷൻ ലോ
മാക്സ് പ്ലാങ്കിന്റെ ഗവേഷണത്തിന് വലിയ പ്രേരണ ആയത് കിർച്ചോഫിൻ്റെ ഒരു കണ്ടെത്തലും തുടർന്ന് ഉയർന്ന ചോദ്യങ്ങളും ആയിരുന്നു. ആ കണ്ടെത്തൽ എന്തെന്ന് ഒന്നു നോക്കാം. അതിന് ആദ്യം emissive power അഥവാ emissivity എന്ന സംഗതിയെ മനസ്സിലാക്കാം. മലയാളത്തിൽ ഇതിൻ്റെ പരിഭാഷയായി ഉത്സർജകത എന്നു കണ്ടിട്ടുണ്ട്. ചൂടുള്ള വസ്തുക്കൾ യൂണിറ്റ് സമയത്തിൽ യൂണിറ്റു പരപ്പളവിൽ (area) നിന്ന് വികിരണങ്ങളായി പുറത്തുവിടുന്ന ഊർജത്തിൻ്റെ അളവാണ് emissive power. നമുക്കതിനെ തത്കാലം \(e\) എന്ന അക്ഷരം കൊണ്ടു സൂചിപ്പിക്കാം. അതിൻ്റെ യൂണിറ്റ് \(Js^{-1}m^{-2}\) ആണ്. ഇതു തന്നെ \(Wm^{-2}\) എന്നും എഴുതാം. ഇതിൽ \(J\)എന്നത് ഊർജത്തിൻ്റെ യൂണിറ്റായ ജൂളിനെയും \(s\) സെക്കൻഡിനെയും \(m\)എന്നത് മീറ്ററിനെയും \(W\) എന്നത് പവറിൻ്റെ യൂണിറ്റായ വാട്ട്സിനെയും സൂചിപ്പിക്കുന്നു. അടുത്തതായി മനസ്സിലാക്കേണ്ടത് അവശോഷണാങ്കം (absorptivity) എന്ന വാക്കാണ്. ഒരു വസ്തുവിൻ്റെ ഉപരിതലത്തിൽ വീഴുന്ന താപവികിരണത്തിൻ്റെ എത്ര ഭാഗം അത് ആഗിരണം ചെയ്യുന്നുവെന്നതിൻ്റെ സൂചകം ആണത്. നമ്മൾ അത് \(a\) എന്ന അക്ഷരം കൊണ്ടു സൂചിപ്പിക്കുന്നു. ഒരു വസ്തു അതിൽ വീഴുന്ന താപത്തിൻ്റെ പകുതിയും ആഗിരണം ചെയ്യുന്നുവെങ്കിൽ \(a= 0.5\) അല്ലെങ്കിൽ \(50\%\). ഒരു ഒന്നാന്തരം ബ്ലാക്ക് ബോഡിയുടെ \(a=100\%\). സാധാരണ വസ്തുക്കളുടെയെല്ലാം \(a\)-യുടെ മൂല്യം പൂജ്യം ശതമാനത്തിനും നൂറു ശതമാനത്തിനും ഇടയിലാകും.
1859-ൽ കിർച്ചോഫ് ഒരു വലിയ കണ്ടെത്തൽ നടത്തി. അത് കിർച്ചോഫിൻ്റെ റേഡിയേഷൻ നിയമം എന്നറിയപ്പെടുന്നു. അത് ഇങ്ങനെ നമുക്ക് പരിഭാഷപ്പെടുത്താം. ഏതൊരു വസ്തുവിൻ്റെയും ഒരു പ്രത്യേക താപനിലയിലും തരംഗദൈർഘൃത്തിലുമുള്ള \(\frac{e}{a}\) മൂല്യം ഒന്നു തന്നെ ആയിരിക്കും. അതായത് കല്ലായാലും കരിക്കട്ട ആയാലും തനി തങ്കമായാലും \(e\) യുടെയും \(a\) യുടെയും അനുപാതം താപനിലയെയും (\(T\)) തരംഗദൈർഘ്യത്തെയും (\(\lambda\)) മാത്രം ആശ്രയിക്കുന്ന ഒരു ഏകദം (function) ആയിരിക്കും. ഗണിതഭാഷയിൽ എഴുതിയാൽ
\begin{equation}
\frac{e}{a}=f(\lambda,T)
\end{equation}
ഇതിൻ്റെ ഒരു തെളിവും (proof) കിർച്ചോഫ് നൽകി. അത് അടുത്ത സെക്ഷനിൽ നൽകുന്നു. അല്പസ്വല്പം ഗണിതം പരിചിതമായിട്ടുള്ളവർക്ക് അതൊന്നു നോക്കാം.
2.2 ഒരു ചിന്താപരീക്ഷണവും കിർച്ചോഫിന്റെ കണ്ടെത്തലും
വലിയ വലിപ്പമുള്ള രണ്ടു പ്ലേറ്റുകളെ സമാന്തരമായി അടുത്തടുത്തു വെച്ചിരിക്കുന്നതായി സങ്കല്പിക്കുക. അവ രണ്ടും വികിരണങ്ങൾ പുറത്തുവിടുകയും ആഗിരണം ചെയ്യുന്നുവെന്നു കരുതുക. അവയിൽ നിന്നു പുറത്തേക്കു പോകുന്ന ഊർജം നല്ല കണ്ണാടികളുടെ സഹായത്തോടെ ഊർജ നഷ്ടമില്ലാതെ തിരിച്ച് അവിടേക്കുതന്നെ വരുന്നുവെന്നും കരുതുക. പ്ലേറ്റുകളുടെ ഉത്സർജകത (emissivity) യഥാക്രമം \(e_1, e_2\)-ഉം അവശോഷണാങ്കം (absorptivity) \(a_1,a_2\)-ഉം പ്രതിപതനാങ്കം (reflectivity) \(r_1, r_2\)-ഉം ആണെന്നു കരുതുക.
ആദ്യത്തെ പ്ലേറ്റിൽ നിന്ന് യൂണിറ്റ് സമയത്ത് യൂണിറ്റ് വിസ്തീർണ്ണത്തിൽ നിന്ന് രണ്ടാം പ്ലേറ്റിൻ്റെ നേരെ വരുന്ന \(e_1\) ഊർജത്തിൻ്റെ ഒരു ഭാഗം, അതായത് \(a_2e_1\) അത് ആഗിരണം ചെയ്യുകയും \(r_2e_1\) തിരിച്ച് ഒന്നാം പ്ലേറ്റിലേക്ക് പ്രതിപതിപ്പിക്കുകയും ചെയ്യും. അതിൻ്റെ ഒരു ഭാഗം, – അതായത് \(a_1r_2e_1\) അത് ആഗിരണം ചെയ്യും. അതോടൊപ്പം \(r_1r_2e_1\) അത് രണ്ടാമത്തെ പ്ലേറ്റിലേക്ക് വീണ്ടും അയക്കും. ഇതിൻ്റെയും ഒരു ഭാഗം, \(r_2r_1r_2e_1\) ഒന്നാം പ്ലേറ്റിലേക്ക് തിരിച്ചുവരികയും അതിൻ്റെ ഒരു ഭാഗം രണ്ടാം പ്ലേറ്റിലേക്ക് തിരിച്ചുവരികയും ചെയ്യും. അത് \(r_1r_2r_1r_2a_1=(r_1r_2)^2e_1\) ആണെന്നത് ആലോചിച്ചാൽ മനസ്സിലാകും. ഇതു വീണ്ടും ആവർത്തിക്കുമ്പോൾ അത് \((r_1r_2)^3e_1\) ആകും. അങ്ങനെ നോക്കുമ്പോൾ പലവട്ടമായി രണ്ടാം പ്ലേറ്റിൽ ആകെ പതിക്കുന്നത്
\begin{equation}
e_1+(r_1r_2)e_1+(r_1r_2)^2e_1+(r_1r_2)^3e_1+ …=\left(1+(r_1r_2)+(r_1r_2)^2+(r_1r_2)^3+…\right)e_1
\end{equation}
ഇതിൽ \((r_1r_2)\) ഒന്നിനേക്കാൾ കുറവായ സംഖ്യ ആയതിനാൽ സീരീസിൻ്റെ തുക എളുപ്പം കണ്ടെത്താം. അതിന് ഈ സമവാക്യം ഉപയോഗിക്കാം:
\begin{equation}
1+x+x^2+x^3+…=\frac{1}{1-x}
\end{equation}
അതായത് രണ്ടാം പ്ലേറ്റിൽ ആകെ പതിക്കുന്നത്.
\begin{equation}
\frac{e_1}{1-r_1r_2}
\end{equation}
ഇത് രണ്ടാം പ്ലേറ്റിൽ പതിക്കുമ്പോൾ അതിൽ നിന്ന് പ്ലേറ്റ് ആഗിരണം ചെയ്യുന്നത്:
\begin{equation}
a_2\times \frac{e_1}{1-r_1r_2} =\frac{a_2e_1}{1-r_1r_2}
\end{equation}
ഇതേ പോലെ രണ്ടാമത്തെ പ്ലേറ്റ് പുറത്തുവിടുന്ന ഊർജത്തിൽ (\(e_1\))-ൽ പല തവണയായി ആദ്യപ്ലേറ്റ് ആഗിരണം ചെയ്യുന്നതിൻ്റെ അളവു കിട്ടാൻ മേൽകൊടുത്ത സമവാക്യത്തിൽ \(1, 2\) എന്നിവ പരസ്പരം മാറ്റിയാൽ മതി. അതായത്,
\begin{equation}
\frac{a_1e_2}{1-r_2r_1}
\end{equation}
രണ്ടു വസ്തുക്കളും താപസന്തുലനത്തിൽ (thermal equilibrium) തുടരണമെങ്കിൽ മുകളിലുള്ള രണ്ടു സമവാക്യങ്ങളിലും ഉള്ള അളവുകൾ തുല്യമാകണം. അതായത്
\begin{equation}
\frac{a_2e_1}{1-r_1r_2}=\frac{a_1e_2}{1-r_2r_1}
\end{equation}
മേൽ സമവാക്യത്തിൽ ഇരുവശത്തേയും ഛേദം (denominator) തുല്യമാണെന്നതു ശ്രദ്ധിക്കുക. അങ്ങനെയെങ്കിൽ അംശവും (numerator) തുല്യമാകണമല്ലോ? അതായത്,
\begin{equation}
a_2e_1=a_1e_2
\end{equation}
ഇരുവശത്തേയും \(a_1a_2\) കൊണ്ടു ഹരിച്ചാൽ നമുക്ക് കിർച്ചോഫിൻ്റെ പ്രിയ സമവാക്യം കിട്ടും;
\begin{equation}
\frac{e_1}{a_1}=\frac{e_2}{a_2}
\end{equation}
ഇനി നമുക്കൊരു കാര്യം ആലോചിക്കാം. നമ്മൾ ഇവിടെ പരിഗണിച്ച രണ്ടു വസ്തുക്കളുമായി താപസന്തുലനത്തിലുള്ള വേറെയും കുറേ വസ്തുക്കൾ പരിഗണിക്കുക. അങ്ങനെയെങ്കിൽ നമുക്ക് ഇങ്ങനെ എഴുതാം:
\begin{equation}
\frac{e_1}{a_1}=\frac{e_2}{a_2}=
\frac{e_3}{a_3}=\frac{e_4}{a_4}=…
\end{equation}
ഇവിടെനമ്മൾ തരംഗദൈർഘ്യത്തിൻ്റെ കാര്യം പറഞ്ഞിരുന്നില്ല. ഏതു തരംഗദൈർഘ്യത്തിലും ഈ സമവാക്യങ്ങൾ ശരിയാകണം. താപസന്തുലനത്തിൽ ആയതിനാൽ വസ്തുക്കളുടെയെല്ലാം താപനിലയും ഒന്നു തന്നെയായിരിക്കണം. അപ്പോൾ ഇതിൽ നിന്നു എത്തുന്ന നിഗമനം \(\frac{e}{a}\) വസ്തുവിൻ്റെ ആകൃതി, വലുപ്പം, നിറം, മൂലക ഘടകങ്ങൾ ഇങ്ങനെയൊന്നുമായും ബന്ധമില്ലാത്ത, തരംഗദൈർഘ്യത്തെയും (\(\lambda\)) താപനിലയെയും (T) മാത്രം ആശ്രയിക്കുന്ന ഒരു സാർവ്വിക ഏകദം (universal function) ആയിരിക്കണം എന്നതാണ്.
\begin{equation}
\frac{e}{a}= f(\lambda, T)
\end{equation}
ഈ ഏകദം (function) കണ്ടെത്തുക എന്നത് ഒരു വെല്ലുവിളി ആയി കിർച്ചോഫ് ശാസ്ത്രലോകത്തിനു മുന്നിൽ വെച്ചു. കിർച്ചോഫിൻ്റെ ജീവിത കാലത്ത് ആർക്കും അതിന് ഉത്തരം നൽകാൻ കഴിഞ്ഞില്ല. 1859-ൽ ഉയർത്തിയ ചോദ്യത്തിന് നാലു ദശകങ്ങൾക്കു ശേഷം 1900-ൽ മാക്സ് പ്ലാങ്ക് ശരിയായ ഉത്തരം നൽകി. ക്വാണ്ട എന്ന ആശയം സയൻസിലേക്കു കടന്നുവന്നത് പ്ലാങ്കിൻ്റെ 1900-ാമാണ്ടിലെ സിദ്ധാന്തത്തിലൂടെയാണ്
2.3 ബ്ലാക്ക് ബോഡി എന്ന ആശയം
ഗുസ്താഫ് കാർച്ചോഫ് (Gustav Kirchhoff) 1860-ൽ അവതരിപ്പിച്ച ആശയമാണ് ബ്ലാക്ക് ബോഡി എന്നത്. ഇതിനെ തമോവസ്തു എന്നൊക്കെ മലയാളത്തിൽ എഴുതാറുണ്ടെങ്കിലും ഇവിടെ കൂടുതൽ പരിചിതമായ ബ്ലാക്ക് ബോഡി എന്ന വാക്കു തന്നെ ഉപയോഗിക്കുന്നു.
വന്നു വീഴുന്ന വികിരണങ്ങളെയാകെ ആഗിരണം ചെയ്യാൻ കഴിയുന്ന ഒരു ആദർശ വസ്തുവാണ് ബ്ലാക്ക് ബോഡി. മറ്റൊരു രീതിയിൽ പറഞ്ഞാൽ അവശോഷണാങ്കം (absorptivity) എന്നത് \(100\%\) ആയിട്ടുള്ള ഒരു വസ്തു.
ബ്ലാക്ക് ബോഡികളെക്കുറിച്ച് ജോസഫ് സ്റ്റെഫൻ (Joseph Stefan, 1835-1893) എന്ന ശാസ്ത്രജ്ഞൻ ഒരു പ്രധാനപ്പെട്ട കണ്ടെത്തൽ നടത്തി. അതനുസരിച്ച് ഒരു ബ്ലാക്ക് ബോഡി യൂണിറ്റ് വിസ്തീർണ്ണത്തിൽ നിന്ന് യൂണിറ്റ് സമയത്തിൽ പുറത്തുവിടുന്ന ഊർജം കേവല താപനിലയുടെ നാലാം ഘാതത്തിന് ആനുപാതികമായിരിക്കും.
\begin{equation}
I=\sigma T^4
\end{equation}
ഇതിലെ സ്ഥിരാങ്കത്തെ സിഗ്മ (\(\sigma\)) എന്ന ഗ്രീക്ക് അക്ഷരം കൊണ്ടു സൂചിപ്പിക്കുന്നു. മറ്റു ചിലരുടെ പരീക്ഷണഫലങ്ങളുടെ വിശകലനം വഴിയാണ് സ്റ്റെഫാൻ 1879-ൽ ഈ നിയമം കണ്ടെത്തിയത്. വിവിധ തരംഗദൈർഘ്യങ്ങളിലുള്ള വികിരണങ്ങളുടെ സംഭാവന എല്ലാം ചേർത്ത് കിട്ടുന്ന ആകെത്തുകയാണിത്. പരീക്ഷണങ്ങളിൽനിന്നു ലഭിക്കുന്ന വിവരങ്ങൾ അനുസരിച്ച് \(\sigma= 5.67\times 10^{-8} Wm^{-2}K^{-4}\). ഈ സമവാക്യം ഉപയോഗിച്ച് സ്റ്റെഫാൻ സൂര്യൻ്റെ ഉപരിതല താപനില \(5700\,K\) എന്ന് സാമാന്യം കൃത്യതയോടെ കണ്ടെത്തി. അകലെയുള്ള നക്ഷത്രങ്ങളുടെ വലുപ്പം കണക്കാക്കാൻ ഇക്കാലത്തും സ്റ്റീഫൻ്റെ നിയമം ഉപയോഗിക്കുന്നു. പിന്നീട് 1884-ൽ സ്റ്റെഫാൻ്റെ ശിഷ്യനായ ബോൾട്സ്മാൻ (Ludwig Boltzmann, 1844-1906) ഇതു സൈദ്ധാന്തികമായി തെളിയിച്ചു. തുടർന്ന് ഇത് സ്റ്റെഫാൻ-ബോൾട്സ്മാൻ നിയമം എന്നും അറിയപ്പെടുന്നു.
സൂര്യന്റെ താപനില നമുക്കും കണ്ടെത്താംസ്റ്റെഫാൻ കണ്ടെത്തിയ പാത പിന്തുടർന്ന് നമുക്കും സൂര്യൻ്റെ ഉപരിതല താപനില (surface temperature) കണ്ടെത്താം. അതിന് സൂര്യൻ ഓരോ സെക്കൻഡിലും പുറത്തുവിടുന്ന വികിരണത്തിലെ ഊർജത്തിൻ്റെ അളവു കണ്ടെത്താം. അതിന് സൂര്യൻ വരെയൊന്നും പോകേണ്ട കാര്യമില്ല. ഭൂമിയിൽ ഇരുന്നു ചെയ്യാം. സൂര്യൻ നേരെ മുകളിൽ വരുമ്പോൾ ഭൂമിയിൽ ഒരു യൂണിറ്റ് വിസ്തീർണത്തിൽ യൂണിറ്റു സമയത്തിൽ വീഴുന്ന വികിരണോർജത്തെ ശാസ്ത്രജ്ഞർ സോളാർ കോൺസ്റ്റൻ്റ് എന്നു വിളിക്കുന്നു. അതിൻ്റെ യൂണിറ്റ് വാട്ട്സ്/ (സ്ക്വയർ മീറ്റർ) ആണ്. അതിൻ്റെ മൂല്യം \(1366\, Wm^{-2}\) ആണ്. ഇവിടെ ഈ നിരക്കിൽ ഊർജം എത്തണമെങ്കിൽ അവിടെ ഏതു നിരക്കിൽ ഉണ്ടാകണം എന്നു നമുക്കു കണക്കാക്കാം. സൂര്യനിൽ നിന്ന് ഭൂമിയിലേക്കുള്ള ശരാശരി ദൂരത്തിനാണ് അസ്ട്രോണമിക്കൽ യൂണിറ്റ് (AU) എന്നു പറയുന്നത്. അത് ഏകദേശം 15 കോടി കിലോമീറ്ററാണ്. മീറ്ററിൽ ആക്കിയാൽ \(1.5\times 10^{11} m\). സൂര്യനിൽ ഉണ്ടാകുന്ന ഊർജം ഒരേ നിരക്കിൽ എല്ലാ ദിശകളിലും തടസ്സങ്ങളില്ലാതെ സഞ്ചരിക്കുന്നു വെന്നു കരുതുക. സൂര്യൻ കേന്ദ്രമായി ഒരു അസ്ട്രോണമിക്കൽ യൂണിറ്റ് റേഡിയസ് ഉള്ള ഒരു ഗോളത്തെ സങ്കല്പിക്കുക. ഈ ഗോളത്തിൻ്റെ വിസ്തീർണ്ണത്തെ (\(4\pi R^2\)) സോളാർ കോൺസ്റ്റൻ്റു കൊണ്ട് പെരുക്കിയാൽ സൂര്യനിൽ ഊർജമുണ്ടാകുന്ന നിരക്ക് കിട്ടും. അതായത്,
\begin{equation}
U= 4\pi\left( 1.5\times 10^{11} m\right)^2\times 1366\, Wm^{-2}=3.862\times 10^{26} W
\end{equation}
ഇതിനെയാണ് സൂര്യൻ്റെ ലൂമിനോസിറ്റി എന്ന് ശാസ്ത്രജ്ഞർ പറയുന്നത്.
ഇനി നമുക്ക് സ്റ്റെഫാൻ കണ്ടെത്തിയ കാര്യത്തിലേക്കുവരാം. അതനുസരിച്ച് സൂര്യൻ്റെ ഉപരിതലത്തിൻ്റെ ഓരോ ചതുരശ്രമീറ്ററിൽ നിന്നും \(\sigma T^4\) എന്ന നിരക്കിൽ ഊർജം പുറത്തു വരണം. സൂര്യൻ്റെ റേഡിയസ് ഏതാണ്ട് 7 ലക്ഷം കിലോമീറ്റർ ആണ് (\(r=7\times 10^8m)\). അതുകൊണ്ട് സൂര്യൻ ആകെ പുറത്തുവിടുന്ന ഊർജം
\begin{equation}
U=\sigma T^4\times 4\pi r^2
\end{equation}
ഇതിൽ നിന്നും ഇങ്ങനെ എഴുതാം;
\begin{equation}
T^4=\frac{U}{\sigma\times 4\pi r^2}
\end{equation}
നമുക്കിനി ഈ സമവാക്യത്തിൽ \(U\), \(\sigma\), \(r\) എന്നിവയുടെ മൂല്യം ചേർത്ത് കണക്കു പൂർത്തിയാക്കാം;
\begin{equation}
T^4=\frac{U}{\sigma\times 4\pi r^2}=\frac{3.862\times 10^{26}}{5.67\times 10^{-8}\times 4\pi (7\times 10^8)^2}=1.106\times 10^{15} K^4
\end{equation}
അങ്ങനെയെങ്കിൽ
\begin{equation}
T=\left( 1.106\times 10^{15} K^4 \right)^\frac{1}{4}
=5767 K\end{equation}
ഇതു യാഥാർത്ഥ്യവുമായി വളരെ അടുത്തു നിൽക്കുന്ന ഒരു സംഖ്യയാണ്.
2.4 വിലെഹം വീനിന്റെ കണ്ടെത്തലുകൾ
വിലെഹം വീൻ (1864-1928) ഒരു പ്രശസ്ത ജർമൻ ശാസ്ത്രജ്ഞനായിരുന്നു. ബ്ലാക്ക് ബോഡി വികിരണവുമായി ബന്ധപ്പെട്ട രണ്ടു കണ്ടെത്തലുകൾ ഇദ്ദേഹത്തിൻ്റെ പേരിലുണ്ട്. ഇതിൽ ഒന്ന് വീൻസ് ഡിസ്പ്ലേസ്മെൻ്റ് ലോ (Wien’s displacement law) എന്നറിയപ്പെടുന്നു. ഒരു ബ്ലാക്ക് ബോഡിയുടെ താപനിലയും (T) അതിൽ നിന്നുവരുന്ന തരംഗങ്ങളിൽ ഏറ്റവും അധികമുള്ളവയുടെ തരംഗദൈർഘ്യവും (\(\lambda\)) തമ്മിലുള്ള ഗുണനഫലം ഒരു സ്ഥിരാങ്കമായിരിക്കുമെന്നതാണ് ഈ നിയമം. ഗണിതത്തിൻ്റെ ഭാഷയിൽ പറഞ്ഞാൽ കാര്യം എളുപ്പമായി;
\begin{equation}
\lambda_{m}T = constant.
\end{equation}
ഇതിലെ സ്ഥിരാങ്കത്തിൻ്റെ (constant) മൂല്യം \(2.89777 \times 10^{-3} \text{മീറ്റർ- കെൽവിൻ}\) എന്നതാണ്. ഇതു പരീക്ഷണങ്ങൾ വഴി ലഭിച്ചതാണ്. ഈ സമവാക്യം ഉപയോഗിച്ചാണ് നമ്മൾ പല വസ്തുക്കളുടേയും താപനില കണ്ടെത്തുന്നത്. ഉദാഹരണമായി സൂര്യപ്രകാശത്തിൻ്റെ കാര്യമെടുത്താൽ അതിൽ ഏറ്റവും കൂടുതൽ ഉള്ള തരംഗങ്ങൾ പച്ചവെളിച്ചത്തിൻ്റേതാണ്. അതിൻ്റെ തരംഗദൈർഘ്യം ഏതാണ്ട് \(500\) നാനോമീറ്റർ. അങ്ങനെയെങ്കിൽ സൂര്യൻ്റെ ഉപരിതല താപനില,
\begin{equation}
T=\frac{2.89777\times 10^{-3} m}{500\, nm}= 5796\, K
\end{equation}
ഇതിനു പുറമേ ബ്ലാക്ക് ബോഡി തരംഗങ്ങളുടെ സ്പെക്ട്രം സംബന്ധിച്ച ഒരു സമവാക്യവും വീനിൻ്റേതായിട്ടുണ്ട് (Wien’s distribution law).
1896-ൽ കിർച്ചോഫിൻ്റെ വെല്ലുവിളിക്ക് ഒരുത്തരം എന്ന രീതിയിൽ ബ്ലാക്ക് ബോഡിയുടെ റേഡിയേഷനെ സംബന്ധിച്ച് അദ്ദേഹം കണ്ടെത്തിയ നിയമം സമവാക്യരൂപത്തിൽ എഴുതിയാൽ ഇങ്ങനെയിരിക്കും:
\begin{equation}
f(\lambda,T)=\frac{a}{\lambda^5}\,e^{-\frac{b}{\lambda T}}
\end{equation}
ഇതു പരീക്ഷണഫലങ്ങളുമായി ഏതാണ്ട് ഒത്തുപോകുന്ന വിധത്തിൽ ഊഹിച്ചെടുത്ത സമവാക്യമായിരുന്നു. കൂടാതെ ഇതു സ്റ്റെഫാൻ-ബോൾട്സ്മാൻ നിയമവുമായും വീനിൻ്റെ തന്നെ ഡിസ്പ്ലേസ്മെൻ്റ് നിയമവുമായും ചേർന്നുപോകുന്നതായിരുന്നു.

ബ്ലാക്ക് ബോഡി വികിരണത്തിൻ്റെ പ്രധാന സ്വഭാവങ്ങൾ ഇതിൽ പ്രതിഫലിക്കുന്നുവെങ്കിലും ഉയർന്ന തരംഗദൈർഘ്യത്തിൽ അത് പരീക്ഷണഫലങ്ങളിൽ നിന്ന് അകൽച്ച കാണിക്കുന്നു. അക്കാലത്ത് ബർലിനിൽ പല ശാസ്ത്രജ്ഞരും ബ്ലാക്ക് ബോഡി ഉപയോഗിച്ചുള്ള പരീക്ഷണങ്ങളിൽ ഏർപ്പെടുന്നുണ്ടായിരുന്നു. അവർക്ക് അധികം താമസിയാതെ മനസ്സിലായ ഒരു കാര്യം വീനിൻ്റെ സമവാക്യങ്ങൾ തരംഗദൈർഘ്യം കൂടിയ വികിരണങ്ങളുടെ കാര്യത്തിൽ പരീക്ഷണ ഫലങ്ങളിൽ നിന്ന് കുറച്ചു വ്യത്യസ്തമായ ഫലങ്ങൾ തരുന്നു എന്നതായിരുന്നു.
എന്നാൽ ഡിസ്പ്ലേസ്മെൻ്റ് ലോ പരീക്ഷണങ്ങളുമായി പൂർണ്ണമായും ഒത്തുപോകുന്നു. ഈ കണ്ടെത്തലുകളുടെ പേരിൽ അദ്ദേഹത്തിന് 1911-ലെ ഫിസിക്സ് നോബെൽ പുരസ്കാരം ലഭിച്ചിട്ടുണ്ട്. പ്ലാങ്കിനെ തൻ്റെ ക്വാണ്ടം സിദ്ധാന്തത്തിലേക്കെത്താൻ വീനിൻ്റെ കണ്ടെത്തലുകൾ ഏറെ സഹായിച്ചിട്ടുണ്ട്.
2. 5 മാക്സ് പ്ലാങ്കിന്റെ കണ്ടെത്തൽ
ബ്ലാക്ക് ബോഡി റേഡിയേഷൻ സംബന്ധിച്ച നിയമം കണ്ടെത്തുക എന്നത് മാക്സ് പ്ലാങ്ക് ഒരു വലിയ വെല്ലുവിളിയായി ഏറ്റെടുത്തിരുന്നു. ഇക്കാര്യത്തിൽ വഴികാട്ടിയായത് കിർച്ചോഫിൻ്റെ കണ്ടെത്തലുകൾ തന്നെ. പ്ലാങ്ക് ആലോചിച്ചത് ഈ വഴിക്കായിരുന്നു; \(\frac{e}{a}\) എന്നത് ഒരു സാർവ്വിക ഏകദം (universal function) ആണ് എന്നതായിരുന്നുവല്ലോ കിർച്ചോഫിൻ്റെ കണ്ടെത്തൽ. ഒരു ബ്ലാക്ക് ബോഡിയുടെ കാര്യത്തിൽ അവശോഷണാങ്കം (absorptivity) \(a=1\) ആയതുകൊണ്ട്, \(\frac{e}{a}=e\). ഉത്സർജകത (emissivity) കണ്ടുപിടിച്ചാൽ മതിയാവും. \(\frac{e}{a}\) ആകട്ടെ ഏതൊരു വസ്തുവിനും ഒന്നുതന്നെയായിരിക്കും എന്ന് കിർച്ചോഫ് തെളിയിച്ചിരുന്നല്ലോ അങ്ങനെയെങ്കിൽ ഒരു ബ്ലാക്ക് ബോഡിയുടെ ഭിത്തി ഉണ്ടാക്കിയിരിക്കുന്നത് ഓസിലേറ്ററുകൾ കൊണ്ടാണ് എന്ന ധാരണയിൽ കണക്കുകൂട്ടാൻ ആണ് പ്ലാങ്ക് ഉദ്ദേശിച്ചത്. ഇവിടെ ഓർക്കേണ്ട ഒരു കാര്യം എല്ലാ വസ്തുക്കളും ആറ്റങ്ങൾ കൊണ്ട് നിർമ്മിതമാണെന്നുള്ള സിദ്ധാന്തം ഒന്നും അന്ന് പൊതുവേ അംഗീകരിക്കപ്പെട്ടിരുന്നില്ല. അതേപോലെ തന്നെ ഇലക്ട്രോണുകളെ സംബന്ധിച്ച ലോറൻസിൻ്റെ സിദ്ധാന്തവും പ്ലാങ്കിന് സ്വീകാര്യമായി തോന്നിയിരുന്നില്ല. എങ്കിലും ഓസിലേറ്ററുകളെ സംബന്ധിച്ച് ഹെർട്സ് നടത്തിയിരുന്ന പഠനങ്ങൾ സഹായകരമായി. അവയെ ബന്ധിപ്പിച്ച് സമവാക്യങ്ങൾ രൂപീകരിച്ചപ്പോൾ അത് പരീക്ഷണഫലങ്ങളുമായി ചേർന്നു പോകുന്നില്ല എന്നത് പ്ലാങ്കിന് ബോധ്യമായി. പിന്നെ എന്ത് ചെയ്യും എന്നതായി ആലോചന. ആ ഇടയ്ക്കാണ് വിലെഹം വീൻ തൻ്റെ സമവാക്യം പ്രസിദ്ധീകരിച്ചത്. ഒറ്റനോട്ടത്തിൽ അത് ശരിയാണ് എന്ന് തോന്നുമെങ്കിലും സൂക്ഷ്മമായ പരീക്ഷണങ്ങൾ അതിനുള്ള വ്യതിയാനം കാണിച്ചു. ജർമ്മനിയിൽ മാക്സ് പ്ലാങ്കിൻ്റെ സുഹൃത്തുക്കൾ തന്നെ ഇതുമായി ബന്ധപ്പെട്ട പരീക്ഷണങ്ങൾ നടത്തുന്നുണ്ടായിരുന്നു.
അങ്ങനെയിരിക്കെ ഒരു ദിവസം രസകരമായ ഒരു സംഭവം ഉണ്ടായി. പ്ലാങ്കിൻ്റെ വീട്ടിൽ
സുഹൃത്തായ ഹൈൻറിക് റുബെൻസ് (Heinrich Rubens) ഒരു ചായയ്ക്കുള്ള ക്ഷണം സ്വീകരിച്ചു കാണാൻ എത്തിയതായിരുന്നു. സംസാരിക്കുന്നതിനിടയിൽ തൻ്റെ പരീക്ഷണത്തിൽ, പ്രത്യേകിച്ചും ഇൻഫ്രാ റെഡ് റീജിയണിൽ കിട്ടിയ ചില റിസൽട്ടുകൾ റുബെൻസ് പ്ലാങ്കിനെ കാണിച്ചു. റുബെൻസ് തിരിച്ചു പോയിട്ടും പ്ലാങ്കിന് അതിനെക്കുറിച്ചു തന്നെയായിരുന്നു ചിന്ത. അന്നു വൈകുന്നേരം തന്നെ പ്ലാങ്കിന് തൻ്റെ പുതിയ സമവാക്യം കിട്ടുകയും അത് ഒരു കത്തിലെഴുതി പോസ്റ്റു ചെയ്യുകയുംചെയ്തത്രേ. അതാണ് പിന്നീട് പ്രസിദ്ധമായ പ്ലാങ്കിൻ്റെ സമവാക്യം.
\begin{equation}
u_\lambda(\lambda,T)=\frac{2hc^2}{\lambda^5}\frac{1}{e^{hc/(\lambda kT)}-1}
\end{equation}
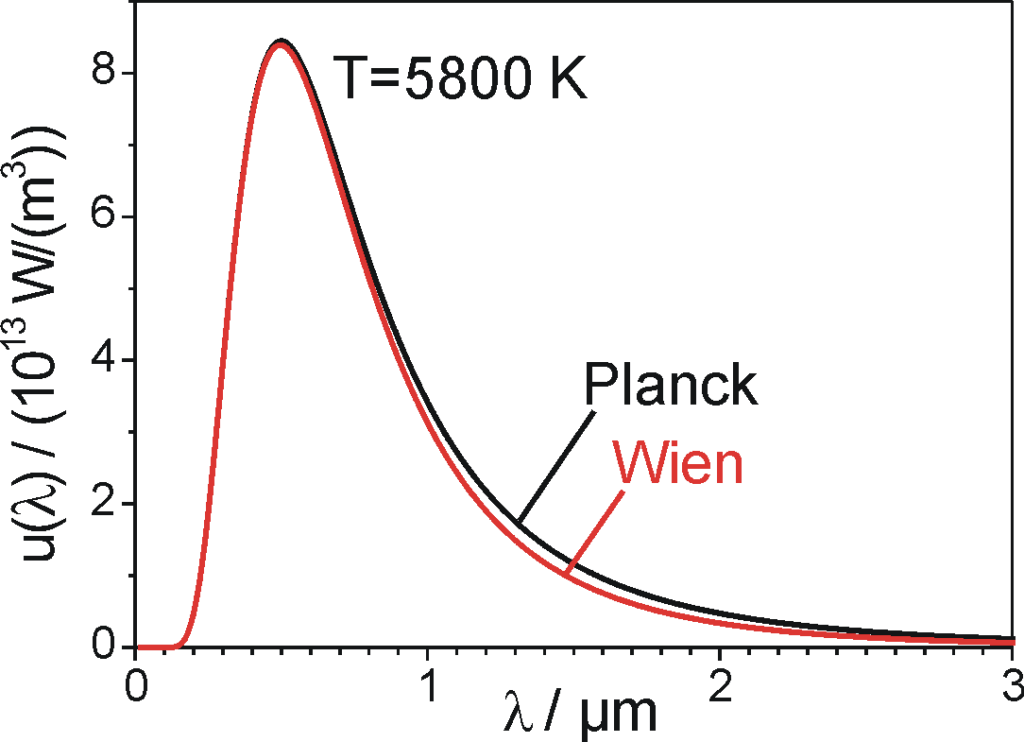
പിന്നീട് നടത്തിയ വിശദമായ പഠനങ്ങളിൽ ഈ സമവാക്യം തികച്ചും ശരിയാണെന്ന് ബോധ്യമായി. ഈ സമവാക്യം രൂപീകരിക്കാൻ പ്ലാങ്കിന് ഒരു അനുമാനം സ്വീകരിക്കേണ്ടിവന്നു. ബ്ലാക്ക് ബോഡി ഊർജം സ്വീകരിക്കുന്നത് \(E=h\nu\) എന്ന അളവിലുള്ള പാക്കറ്റുകളായാണ് എന്നതായിരുന്നു അത്. ഇതിനെയാണ് നമ്മൾ ക്വാണ്ടം (ബഹുവചനം ക്വാണ്ട) എന്നു പറയുന്നത്. ഇതിലെ \(h\) എന്ന സ്ഥിരാങ്കമാണ് പിന്നീട് പ്ലാങ്കിൻ്റെ സ്ഥിരാങ്കം എന്നറിയപ്പെടുന്നത്. ഇതിനു പ്ലാങ്ക് കണക്കാക്കിയ മൂല്യം \(6.55\times 10^{-34}Js\) ആണ്. ഇപ്പോൾ ശാസ്ത്രജ്ഞർ ഉപയോഗിക്കുന്ന മൂല്യം \( 6.62607015\times 10^{-34} Js\) എന്നതാണ്. രണ്ടും തമ്മിലുള്ള വ്യത്യാസം \(1.2\%\) മാത്രം.
ക്വാണ്ടം കോഴ്സിന്റെ ഭാഗമായി ഇതുവരെ പങ്കിട്ട കുറിപ്പുകൾ
