ക്വാണ്ടംമെക്കാനിക്സിലേക്ക് നയിച്ച സംഭവപരമ്പരകളിൽ പ്രധാനപ്പെട്ട ഒന്നായിരുന്നു നീൽസ് ബോർ അവതരിപ്പിച്ച ആറ്റം മോഡെൽ. അതിൻ്റെ ഒരു ഘട്ടത്തിന്റെ തുടക്കം ഇലക്ട്രോണിന്റെ കണ്ടെത്തൽ ആയിരുന്നുവെന്നു പറയാം. 19-ാം നൂറ്റാണ്ടിന്റെ അവസാനകാലത്ത് നടന്ന കുറേയേറെ പരീക്ഷണങ്ങളുടെ ഒടുവിൽ ജെ.ജെ. തോംസൺ (J.J. Thomson, 1856-1940) ചില പ്രധാന കണ്ടുപിടുത്തങ്ങൾ നടത്തി.
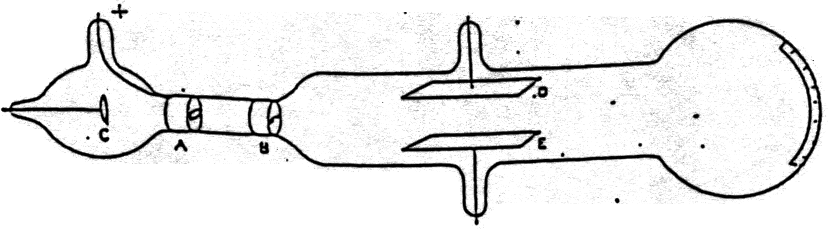
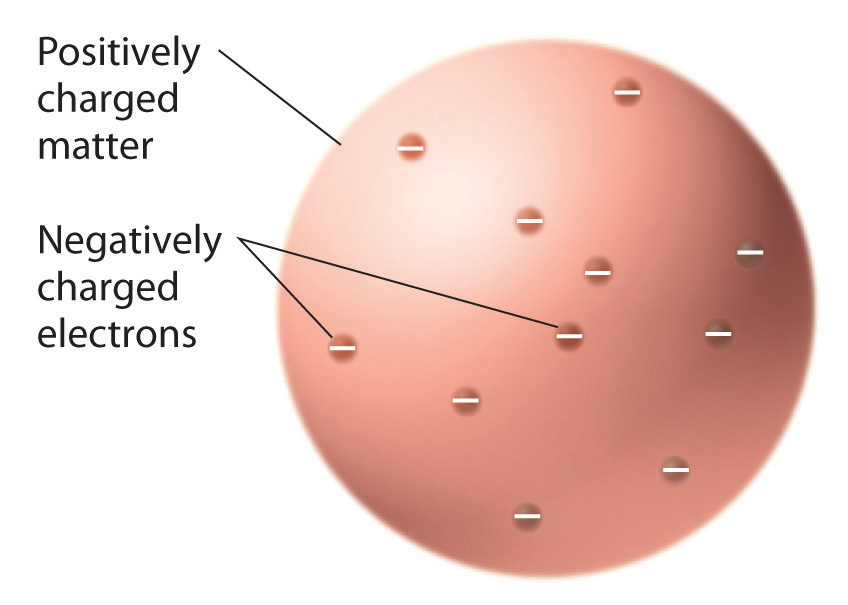
കാഥോഡ് റേ ട്യൂബുകളിൽ ഒഴുകിനടക്കുന്ന കണങ്ങൾ വിവിധതരം വാതകങ്ങളിലെല്ലാം പൊതുവായി അടയങ്ങിയിരിക്കുന്ന ചാർജുള്ള ഒരിനം കണികകളാണ്. അവ ഇലക്ട്രിക് ഫീൽഡിൽ ദിശാവ്യതിയാനം സംഭവിക്കുന്നവയാണ്. അവയുടെ ചാർജിൻ്റെയോ മാസിൻ്റെയോ അളവ് പ്രത്യേകം കണ്ടെത്താൻ കഴിഞ്ഞില്ലെങ്കിലും രണ്ടിൻ്റെയും അനുപാതം കണ്ടെത്താൻ തോംസണു കഴിഞ്ഞു. ഈ കണമാണ് ഇന്നു നമുക്കു പ്രിയപ്പെട്ട ഇലക്ട്രോൺ. ലഭിച്ച വിവരങ്ങളുടെ അടിസ്ഥാനത്തിൽ തോംസൺ മുന്നോട്ടു വെച്ച മാതൃക പ്ലം-പുഡ്ഡിംഗ് (plum pudding) മാതൃക എന്നറിയപ്പെട്ടു. പോസിറ്റീവ് ചാർജുള്ള ദ്രവ്യത്തിൻ്റെ ഇടയിൽ നെഗറ്റീവ് ചാർജുള്ള ധാരാളം ഇലക്ട്രോണുകൾ വിന്യസിക്കപ്പെട്ടിരിക്കുന്നു എന്നതായിരുന്നു ആ മാതൃക. പ്രോട്ടോൺ, ന്യൂട്രോൺ എന്നീ കണങ്ങൾ അടങ്ങിയ ന്യൂക്ലിയസിനെക്കുറിച്ച് അന്ന് യാതൊരു ധാരണയും ഇല്ലായിരുന്നു. ഇന്ന് തിരിഞ്ഞു നോക്കുമ്പോൾ തോംസണിൻ്റെ ആറ്റം മാതൃകയ്ക്ക് ചരിത്രപരമായ പ്രാധാന്യം മാത്രമാണുള്ളത്.
ഇലക്ട്രോണിന്റെ കണികാസ്വഭാവം തെളിയിച്ച ജെ.ജെ. തോംസണിന് 1906-ലെ ഫിസിക്സ് നോബെൽ പുരസ്കാരം ലഭിച്ചു. പിന്നീട് ഇലക്ട്രോണിന്റെ തരംഗ സ്വഭാവം തെളിയിച്ച അദ്ദേഹത്തിന്റെ മകൻ ജി.പി, തോംസണിന് നോബെൽ പുരസ്കാരം ലഭിച്ചിട്ടുണ്ട്. മികച്ച ഒരു അദ്ധ്യാപകൻ കൂടി ആയിരുന്ന ജെ. ജെ.യുടെ 7 വിദ്യാർത്ഥികൾക്ക് നോബെൽ പുരസ്കാരം ലഭിച്ചിട്ടുണ്ട്. അതിലൊരാളായ റഥർഫോർഡ് ആണ് ആറ്റം മാതൃകളുടെ കാര്യത്തിൽ അടുത്ത മുന്നേറ്റം സൃഷ്ടിച്ചത്.

ആറ്റങ്ങൾക്കെല്ലാം പോസിറ്റീവ് ചാർജ് അടങ്ങിയ ഒരു ന്യൂക്ലിയസ് ഉണ്ടെന്ന് സ്ഥാപിക്കുക വഴി ന്യൂക്ലിയർ ഫിസിക്സിന് തുടക്കം കുറിച്ച ശാസ്ത്രജ്ഞനായിരുന്നു ഏണസ്റ്റ് റഥർഫോർഡ് (Ernest Rutherford, 1871-1937). അദ്ദേഹം റേഡിയോ ആക്ടിവിറ്റിയുമായി ബന്ധപ്പെട്ട് നടത്തിയ പരീക്ഷണങ്ങളാണ് ഇതിലേക്ക് നയിച്ചത്. റേഡിയോ ആക്ടിവ് വസ്തുക്കൾ ആൽഫ, ബീറ്റ എന്നിങ്ങനെ രണ്ടിനം കണങ്ങളെ പുറത്തുവിടുന്നുണ്ടെന്ന് കണ്ടെത്തിയതും അവയ്ക്ക് ആ പേരുകൾ നൽകിയതും റഥർഫോർഡായിരുന്നു. റേഡിയോ ആക്റ്റിവിറ്റിയുമായി ബന്ധപ്പെട്ട ഗവേഷണങ്ങളുടെ പേരിൽ 1908-ൽ കെമിസ്ട്രി നോബെൽ പുരസ്കാരം നേടിയ ശേഷമാണ് റഥർഫോർഡ് നമ്മൾ ചർച്ച ചെയ്യാൻ പോകുന്ന കണ്ടെത്തലുകൾ നടത്തിയത് എന്നത് ശ്രദ്ധിക്കേണ്ട കാര്യമാണ്. 1909 – മുതൽ റഥർഫോർഡിൻ്റെ മേൽനോട്ടത്തിൽ ഹാൻസ് ഗീഗർ (Hans Geiger), ഏണസ്റ്റ് മാർസ്ഡെൻ (Ernest Marsden) എന്നിവരാണ് ബന്ധപ്പെട്ട പരീക്ഷണങ്ങൾ നടത്തിയത്. ഈ പരീക്ഷണം തുടങ്ങുന്ന കാലത്ത് മാർസ്ഡെൻ 20 വയസ്സുള്ള ഒരു വിദ്യാർത്ഥിയായിരുന്നു.
പരീക്ഷണം ഇതായിരുന്നു; ഒരു റേഡിയോ ആക്ടിവ് സ്രോതസ്സിൽ നിന്ന് ഉയർന്ന ഊർജമുള്ള ആൽഫാ കണങ്ങളെ വളരെ നേർത്ത ഒരു സ്വർണ്ണ പാളിയിൽ വീഴിക്കുന്നു. ഇവിടെ ആൽഫാ കണങ്ങളുടെ സ്രോതസ്സായി ഉപയോഗിച്ചത് റേഡിയം ആയിരുന്നു.
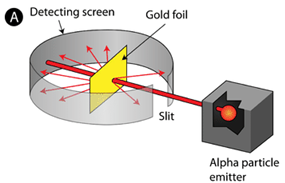
റേഡിയത്തിൽ നിന്ന് പുറത്തുവരുന്ന ആൽഫാ കണങ്ങൾക്ക് ഏതാണ്ട് \(5\,MeV\) ഊർജമുണ്ടാകും. ആ കണങ്ങളുടെ വേഗമാകട്ടെ സെക്കൻഡിൽ 15000 കിലോമീറ്ററും. ഈ ഊർജമുള്ള ആൽഫാ കണങ്ങൾ എല്ലാം സ്വർണപാളിയെ തുളച്ച് അപ്പുറത്തേക്ക് പോകുമെന്നാണ് അവർ കരുതിയത്. മിക്കവാറും ആൽഫാ കണങ്ങളുടെ കാര്യത്തിൽ അതു തന്നെയാണ് സംഭവിച്ചതും. എന്നാൽ വളരെ കുറഞ്ഞ അളവിൽ ചില ആൽഫാ കണങ്ങൾ സ്വർണ്ണ പാളിയിൽ നിന്ന് തിരിച്ച് വരുന്നതായി അവർ കണ്ടെത്തി. ഇത് അത്ഭുതകരമായിരുന്നു. റഥർഫോർഡിന്റെ തന്നെ വാക്കുകളിൽ പറഞ്ഞാൽ,
Then I remember two or three days later, Geiger coming to me in great excitement and saying, “We have been able to get some of the alpha particles coming backwards…”. It was quite the most incredible event that has ever happened to me in my life. It was almost as incredible as if you fired a 15-inch shell at a piece of tissue paper and it came back and hit you. On consideration, I realised that this scattering backward must be the result of a single collision, and when I made calculations I saw that it was impossible to get anything of that order of magnitude unless you took a system in which the greater part of the mass of the atom was concentrated in a minute nucleus. It was then that I had the idea of an atom with a minute massive centre, carrying a charge.
പോസിറ്റീവ് ചാർജും സാമാന്യം മാസും ഉള്ള ആൽഫാ കണത്തെ തിരിച്ചുവിടാനുള്ള ബലം ചെലുത്താൻ പോസിറ്റീവ് ചാർജും നല്ല സാന്ദ്രതയും ഉള്ള കേന്ദ്രം വേണമെന്ന് റഥർഫോർഡ് മനസ്സിലാക്കി.
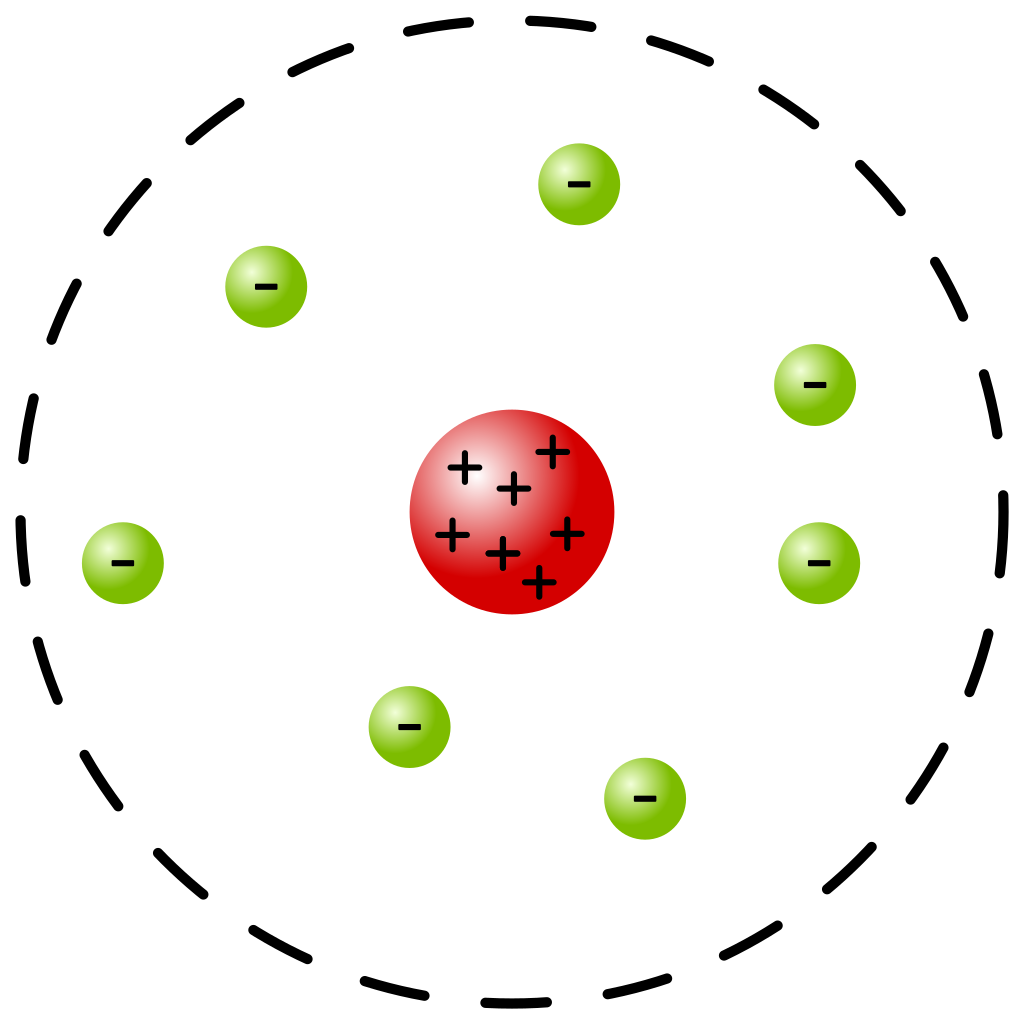
തുടർന്ന് റഥർഫോർഡ് അവതരിപ്പിച്ച ആറ്റം മാതൃകയനുസരിച്ച് ആറ്റങ്ങൾക്കെല്ലാം വളരെ ചെറിയ പോസിറ്റീവ് ചാർജുള്ള ഒരു ന്യൂക്ലിയസ് ഉണ്ട്. ഇലക്ട്രോണുകൾ അതിനു ചുറ്റും കറങ്ങിക്കൊണ്ടിരിക്കുന്നു. സൂര്യനു ചുറ്റും ഗ്രഹങ്ങൾ ഗുരുത്വാകർഷണ ബലത്താൽ സഞ്ചരിക്കുന്നതുപോലെ ഇലക്ട്രോണുകൾ ന്യൂക്ലിയസിനു ചുറ്റും തിരിയുന്നു എന്ന ഈ മാതൃക തോംസൺ മാതൃകയേക്കാൾ മികച്ചതായിരുന്നു. പക്ഷേ, ഒരു സൈദ്ധാന്തിക പ്രശ്നം നിലവിലുണ്ടായിരുന്നു.
ക്ലാസ്സിക്കൽ ഇലക്ട്രോഡൈനാമിക്സിൻ്റെ തത്വങ്ങൾ അനുസരിച്ച് ന്യൂക്ലിയസിനു ചുറ്റും സഞ്ചരിക്കുന്ന ഇലക്ട്രോണുകൾ വിദ്യുത്കാന്തികതരംഗങ്ങൾ പുറത്തുവിടുകയും അതുവഴി ഊർജം നഷ്ടപ്പെടുത്തി ന്യൂക്ലിയസിലേക്കുപതിക്കുകയും ചെയ്യും. അതായത്, ആറ്റങ്ങൾക്ക് നിലനില്പ് ഉണ്ടാവില്ല. ഇതു കൂടാതെ ആറ്റങ്ങൾ പുറത്തുവിടുന്നത് ഏതൊക്കെ തരംഗങ്ങൾ, എത്ര അളവിൽ എന്നൊന്നും പ്രവചിക്കാൻ റഥർഫോർഡിൻ്റെ മോഡെലിനു സാധിച്ചില്ല.
4.1 ബോർ ആറ്റം മോഡൽ

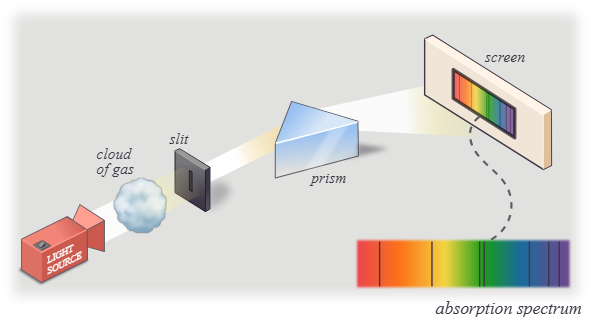
1911-18 കാലഘട്ടത്തിൽ നീൽസ് ബോർ (Niels Bohr, 1885-1962) എന്ന ശാസ്ത്രജ്ഞൻ റഥർഫോർഡിൻ്റെ മാതൃകയിൽ ചില നിബന്ധനകൾ കൂടി കൂട്ടിച്ചേർത്ത് സൃഷ്ടിച്ച ഈ മാതൃകയ്ക്ക് പല കാര്യങ്ങളും വിശദീകരിക്കാൻ കഴിഞ്ഞു. അതിൽ പ്രധാനപ്പെട്ട ഒന്നായിരുന്നു ഹൈഡ്രജൻ്റെ സ്പെക്ട്രം. ഉത്തേജിത അവസ്ഥയിലുള്ള ഹൈഡ്രജൻ ആറ്റങ്ങൾ പുറത്തുവിടുന്ന വെളിച്ചത്തെ ഒരു പ്രിസത്തിലൂടെ കടത്തി വിട്ടാൽ അതിൽ പലതരത്തിലുള്ള ലൈനുകൾ കാണാൻ കഴിയും. ഇതാണ് ഹൈഡ്രജൻ്റെ എമിഷൻ സ്പെക്ട്രം. ഇതിനു പകരം ധവള പ്രകാശത്തെ ഹൈഡ്രജൻ വാതകത്തിലൂടെ കുത്തി വിട്ടതിനു ശേഷം ഒരു പ്രിസത്തിൽ പതിപ്പിച്ചാൽ അതിൽ ചില ഇരുണ്ട ലൈനുകൾ കാണും. ഇതാണ് അവശോഷണ സ്പെക്ട്രം അഥവാ അബ്സോർപ്ഷൻ സ്പെക്ട്രം.
ആറ്റങ്ങളുടെ സ്പെക്ട്രം വിശദീകരിക്കാൻ ശ്രമിച്ച റിഡ്ബെർഗ് (Johannes Rydberg, 1854-1912) എന്ന ശാസ്ത്രജ്ഞൻ രസകരമായ ഒരു സമവാക്യം കണ്ടെത്തി. അത് ഇങ്ങനെ എഴുതാം;
\begin{equation}{\label{Rydberg formula}}
\frac{1}{\lambda}=R\left( \frac{1}{n_1^2}-\frac{1}{n_2^2}
\right)
\end{equation}
ഇതിൽ \(\lambda\) എന്നത് തരംഗദൈർഘ്യം, \(R\) എന്നത് റിഡ്ബെർഗ് സ്ഥിരാങ്കം, \(n_1\), \(n_2\) എന്നിവ എണ്ണൽ സംഖ്യകൾ. കൂടാതെ \(n_2>n_1\).
പരീക്ഷണഫലങ്ങളുടെ അടിസ്ഥാനത്തിലാണ് റിഡ്ബെർഗ് ഈ സമവാക്യം എഴുതിയത്. എന്നാൽ ഇതിനൊരു നല്ല വിശദീകരണം നൽകാനും സ്ഥിരാങ്കത്തിൻ്റെ മൂല്യം ഗണിച്ചെടുക്കാനും നീൽസ് ബോറിനു കഴിഞ്ഞു എന്നത് വലിയ നേട്ടമായി.
അതിനായി നീൽസ് ബോർ ചില നിബന്ധനകൾ മുന്നോട്ടുവെച്ചു. അവ ഇങ്ങനെ എഴുതാം.
1. ആറ്റങ്ങൾക്ക് ചില പ്രത്യേക ഊർജനിലകൾ മാത്രമാണ് അനുവദനീയമായിട്ടുള്ളത്.
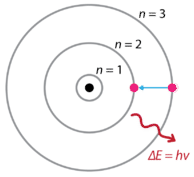
2. ആ ഊർജനിലകളിൽ ഇലക്ട്രോണിൻ്റെ കോണീയ സംവേഗം (angular momentum) \(=n\frac{h}{2\pi}\). ഇതിൽ \(h=\) പ്ലാങ്ക് സ്ഥിരാങ്കം. \(n= 1, 2, 3,…\)
3. ആ ഊർജനിലകളിൽ ഇലക്ട്രോണുകൾ സ്റ്റേബിൾ ആയിരിക്കും.
4. ഇലക്ട്രോൺ ഉയർന്ന ഊർജനിലയിൽ നിന്നും ഊർജം കുറഞ്ഞ നിലയിലേക്കു പോകുമ്പോൾ ഒരു പ്രകാശകണത്തെ പുറത്തുവിടും.
ഈ മാതൃകയനുസരിച്ച് കണക്കുകൂട്ടലുകൾ നടത്തുകയാണെങ്കിൽ തരംഗദൈർഘ്യത്തിന് നമുക്കു കിട്ടുന്ന സമവാക്യം ഇതാണ്.
\begin{equation}
\frac{1}{\lambda}=\frac{me^4}{8\varepsilon_0^2h^3c}\left( \frac{1}{n_1^2}-\frac{1}{n_2^2}
\right)
\end{equation}
നീൽസ് ബോറിൻ്റെ ഈ സമവാക്യം റിഡ്ബെർഗിൻ്റെ സമവാക്യം തന്നെയാണെന്നുള്ളതാണ് ഇതിൻ്റെ ശക്തി. ഈ സമവാക്യം എങ്ങനെ ലഭിക്കുന്നുവെന്നതിൻ്റെ വിശദാംശം അടുത്ത സെക്ഷനിൽ കൊടുക്കുന്നു.
4.2 നീൽസ് ബോറിൻ്റെ സിദ്ധാന്തം ഗണിതത്തിൻ്റെ ഭാഷയിൽ
നീൽസ് ബോറിൻ്റെ സിദ്ധാന്തം അനുസരിച്ച് ആറ്റത്തിൻ്റെ കേന്ദ്രത്തിൽ ന്യൂക്ലിയസ് സ്ഥിതി ചെയ്യുന്നു. ഹൈഡ്രജൻ ആറ്റത്തിൻ്റെ കാര്യത്തിൽ ഇത് ഒരു പ്രോട്ടോൺ മാത്രം അടങ്ങിയതാണ്. അതിന് പോസിറ്റീവ് ചാർജ് ഉണ്ട്. ആ ചാർജിൻ്റെ മൂല്യം ഇലക്ട്രോണിൻ്റെ ചാർജിനോട് തുല്യമാണ്. അത് \(e\) എന്ന് നമുക്ക് എടുക്കാം. പ്രോട്ടോണും ഇലക്ട്രോണും തമ്മിൽ കൂളോം (Coulomb) നിയമമനുസരിച്ച് ഒരു ബലം പ്രവർത്തിക്കുന്നു. അതിൻ്റെ സമവാക്യം ഇതാണ്;
\begin{equation}\label{Coulomb law}
F=k\frac{e^2}{r^2}
\end{equation}
ഇതിൽ \(r\) എന്നത് പ്രോട്ടോണും ഇലക്ട്രോണും തമ്മിലുള്ള ദൂരത്തെ സൂചിപ്പിക്കുന്നു, \(k\) എന്നത് ഒരു സ്ഥിരാങ്കമാണ്. SI യൂണിറ്റിൽ അതിൻ്റെ മൂല്യം, \(k=\frac{1}{4\pi\varepsilon_0}\) ഇതിൽ \( \,\varepsilon_0= \) പെർമിറ്റിവിറ്റി.
ഈ ബലമാണ് ഇലക്ട്രോണിനെ അതിൻ്റെ ഓർബിറ്റിൽ നിർത്തുന്നത്. ന്യൂട്ടൻ്റെ രണ്ടാം നിയമമനുസരിച്ച് ഒരു ബലം ഉണ്ടെങ്കിൽ അത് ത്വരണം ഉണ്ടാക്കും. രണ്ടാം നിയമം ഗണിത രൂപത്തിൽ എഴുതിയാൽ
\begin{equation}
F=ma
\end{equation}
ഒരു ഇലക്ട്രോൺ \(r\) റേഡിയസ് ഉള്ള വൃത്തപഥത്തിലൂടെ \(v\) വേഗത്തിൽ സഞ്ചരിക്കുമ്പോൾ കേന്ദ്രത്തിന് നേരെയുള്ള ത്വരണത്തിൻ്റെ സമവാക്യം;
\begin{equation}
a=\frac{v^2}{r}.
\end{equation}
മുകളിലെ രണ്ടു സമവാക്യങ്ങളും ചേർത്താൽ,
\begin{equation}\label{second law}
F=m\frac{v^2}{r}.
\end{equation}
ബലവുമായി ബന്ധപ്പെട്ട സമവാക്യങ്ങൾ താരതമ്യം ചെയ്താൽ;
\begin{equation}\label{mvsquaredbyr}
m\frac{v^2}{r}=k\frac{e^2}{r^2}.
\end{equation}
ഈ സമവാക്യത്തിൽ ഇരു വശത്തും ഛേദത്തിലുള്ള ഒരു \(r\)-നെ റദ്ദു ചെയ്താൽ,
\begin{equation}\label{mvsquared}
mv^2=k\frac{e^2}{r}.
\end{equation}
ഇനി നമുക്ക് ഊർജത്തിൻ്റെ കാര്യം പരിഗണിക്കാം. ഇവിടെ പ്രോട്ടോണിനെ ചുറ്റുന്ന ഇലക്ട്രോണിൻ്റെ ഗതികോർജം (kinetic energy) \(\frac{1}{2}mv^2\) ആണ്. കൂടാതെ പ്രോട്ടോൺ-ഇലക്ട്രോൺ സിസ്റ്റത്തിൻ്റെ പൊട്ടൻഷ്യൽ ഊർജം \(-k\frac{e^2}{r} \) ആണ്. രണ്ടും ചേർത്ത് എഴുതിയാൽ ആകെ ഊർജം,
\begin{equation}
E=\frac{1}{2}mv^2-k\frac{e^2}{r}
\end{equation}
തൊട്ടു മുകളിലെ സമവാക്യത്തെ ഇവിടെ ചേർത്താൽ,
\begin{equation}\label{bohrenergy}
E=\frac{1}{2}k\frac{e^2}{r}-k\frac{e^2}{r}=-\frac{1}{2}k\frac{e^2}{r}
\end{equation}
അതായത് ആകെ ഊർജം പൊട്ടെൻഷ്യൽ ഊർജത്തിൻ്റെ പകുതിയാണ്. അടുത്തതായി നമുക്ക് നീൽസ് ബോറിൻ്റെ ക്വാണ്ടം നിബന്ധന പരിഗണിക്കാം. അതായത്, കോണീയ സംവേഗം,
\begin{equation}
mvr=n\frac{h}{2\pi}
\end{equation}
ഇതിൽ നിന്നും
\begin{equation}
v=\frac{nh}{2\pi mr}
\end{equation}
വേഗത്തിനുള്ള ഈ സമവാക്യത്തെ \( \frac{mv^2}{r}\)-ൻ്റെ സമവാക്യത്തിൽ ചേർത്താൽ,
\begin{equation}
m\frac{\left(\frac{nh}{2\pi mr}\right)^2}{r}=k\frac{e^2}{r^2}.
\end{equation}
അതായത്
\begin{equation}
\frac{mn^2h^2}{4\pi^2m^2r^3}=k\frac{e^2}{r^2}.
\end{equation}
ഇതു ലളിതവത്കരിച്ച് ഇങ്ങനെയും എഴുതാം;
\begin{equation}
\frac{1}{r}=\frac{4\pi^2kme^2}{n^2h^2}
\end{equation}
ഇതു ഊർജത്തിനുള്ള സമവാക്യത്തിൽ ചേർത്താൽ
\begin{equation}
E=-\frac{1}{2}ke^2\times \frac{1}{r}=-\frac{1}{2}ke^2\times \frac{4\pi^2kme^2}{n^2h^2}=-\frac{2\pi^2k^2me^4}{n^2h^2}.
\end{equation}
ഇവിടെഒരു കാര്യം ശ്രദ്ധിക്കുക. സമവാക്യത്തിൻ്റെ വലതു ഭാഗത്തുള്ളവയിൽ \(n^2\) ഒഴികെയുള്ളതെല്ലാം സ്ഥിരാങ്കങ്ങളാണ്. \(n\)-ൻ്റെ മൂല്യമാകട്ടെ \(n=1, 2, 3, …\) എന്നിങ്ങനെയാണ്. \(n\)-ൻ്റെ മൂല്യം മാറുന്നതനുസരിച്ച് \(E\)- യുടെ മൂല്യവും മാറും. അതു സൂചിപ്പിക്കാൻ നമുക്ക് ഇങ്ങനെ എഴുതാം;
\begin{equation}
E_n=-\frac{2\pi^2k^2me^4}{h^2}\times \frac{1}{n^2}.
\end{equation}
ഇതിൽ സ്ഥിരാങ്കങ്ങളുടെ മൂല്യമെല്ലാം നൽകി ഊർജത്തെ കണക്കാക്കി അത് ഇലക്ട്രോൺ വോൾട്ട് രൂപത്തിൽ എഴുതിയാൽ;
\begin{equation}
E_n=-\frac{13.6\,eV}{n^2}
\end{equation}
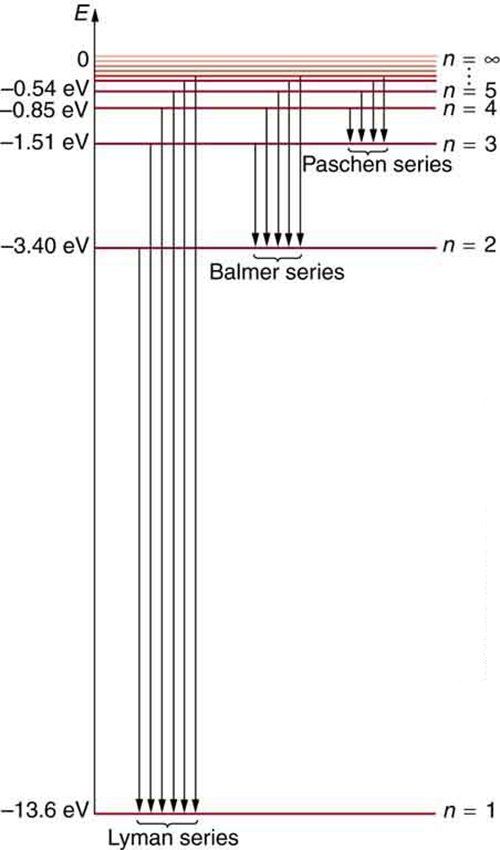
ഇതിൽ \(n=1\) എന്നു കൊടുത്താൽ ലഭിക്കുന്നത് \(E_1=-13.6\,eV\). ഇത് ഗ്രൗണ്ട് സ്റ്റേറ്റ് എനർജി എന്നറിയപ്പെടുന്നു. ഇതാണ് ഹൈഡ്രജൻ ആറ്റത്തിനു സാദ്ധ്യമാവുന്ന മിനിമം എനർജി. സമവാക്യത്തിൽ \(n=2\) കൊടുത്താൽ \(E_2=-3.4\, eV\) ആണ് ആദ്യത്തെ ഉത്തേജിത അവസ്ഥയുടെ (first excited state) ഊർജം.
അങ്ങനെയെങ്കിൽ \(n=2\) ഊർജനിലയിൽ നിന്ന് \(n=1\) ഊർജനിലയിലേക്ക് ഇലക്ട്രോൺ പതിക്കുമ്പോൾ പുറത്തുവരുന്ന പ്രകാശകണത്തിൻ്റെ ഊർജം, \(E_2-E_1=-3.4\,eV-(-13.6\,eV)=10.2\,eV\). ഇത്രയും ഊർജമുള്ള ഒരു ഫോട്ടോൺ ആയിരിക്കും പുറത്തേക്കു വരിക. ഇത് അൾട്രാവയലറ്റ് മേഖലയിൽ ആയിരിക്കുമെന്നതിനാൽ നമുക്കു കാണാൻ കഴിയില്ല.
ഹൈഡ്രജൻ ആറ്റത്തിൽ \(n_2\) ഊർജനിലയിൽ നിന്നും \(n_1\) ഊർജനിലയിലേക്ക് ഇലക്ട്രോൺ നിങ്ങുമ്പോൾ പുറത്തുവരുന്ന പ്രകാശകണത്തിൻ്റെ ഊർജം,
\begin{equation}
h\nu= E_{n_2}- E_{n_1}=\frac{2\pi^2k^2me^4}{h^2}\times \left( \frac{1}{n_1^2}-\frac{1}{n_2^2} \right).
\end{equation}
പ്രകാശത്തിൻ്റെ വേഗം \(c=\nu\lambda\) ആയതിനാൽ \(\nu=\frac{c}{\lambda}\). അങ്ങനെയെങ്കിൽ,
\begin{equation}
\frac{hc}{\lambda}=\frac{2\pi^2k^2me^4}{h^2}\times \left( \frac{1}{n_1^2}-\frac{1}{n_2^2} \right).
\end{equation}
ഈ സമവാക്യത്തിൻ്റെ ഇരു ഭാഗത്തെയും \(hc\) കൊണ്ടു ഹരിച്ചാൽ നമുക്ക് റിഡ്ബെർഗിൻ്റെ സമവാക്യം കിട്ടും:
\begin{equation}
\frac{1}{\lambda}=\frac{2\pi^2k^2me^4}{h^3c}\times \left( \frac{1}{n_1^2}-\frac{1}{n_2^2} \right)=R\left( \frac{1}{n_1^2}-\frac{1}{n_2^2} \right).
\end{equation}
SI യൂണിറ്റുകൾ ഉപയോഗിക്കുമ്പോൾ \(k=\frac{1}{4\pi\varepsilon_0}\) ആണ് എന്നതു കൂടി ഉപയോഗിച്ചാൽ;
\begin{equation}
\frac{1}{\lambda}=\frac{me^4}{8\varepsilon_0^2h^3c}\times \left( \frac{1}{n_1^2}-\frac{1}{n_2^2} \right).
\end{equation}
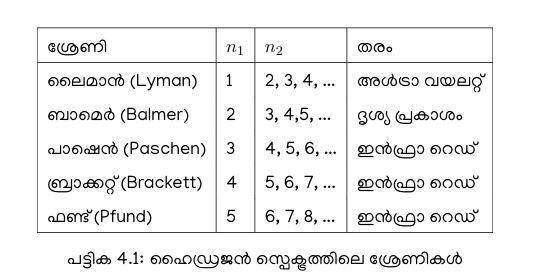
ഇതിൽ താഴെയുള്ള \(n_1\) ലെവലിൻ്റെ മൂല്യം അനുസരിച്ച് സ്പെക്ട്രത്തെ വിവിധ ശ്രേണികളാക്കാം.
ഓരോ ശ്രേണിക്കും പിന്നിലുള്ള ഇലക്ട്രോൺ `ചാട്ടങ്ങൾ’ ഏതെന്ന് അടുത്ത ചിത്രത്തിൽ കാണാം.
നീൽസ്ബോറിൻ്റെ ഈ ആറ്റം മാതൃക വലിയ പ്രശംസ പിടിച്ചു പറ്റി. 1922-ലെ നോബെൽ പുരസ്കാരം അദ്ദേഹത്തിനാണ് ലഭിച്ചത്. പക്ഷേ, ഈ മാതൃകയ്ക്ക് ചില പോരായ്മകൾ ഉണ്ടായിരുന്നു. ആവർത്തന പട്ടികയിൽ ഹൈഡ്രജൻ കഴിഞ്ഞുള്ള മൂലകങ്ങളുടെ കാര്യത്തിൽ ഊർജനിലകളും സ്പെക്ട്രത്തിൻ്റെ വിശദാംശങ്ങളും പ്രവചിക്കാൻ കഴിഞ്ഞിരുന്നില്ല എന്നതായിരുന്നു ഒരു പ്രധാന പോരായ്മ.
ക്വാണ്ടം കോഴ്സിന്റെ ഭാഗമായി ഇതുവരെ പങ്കിട്ട കുറിപ്പുകൾ
