5.1 ഫ്രാങ്ക്-ഹെർട്സ് പരീക്ഷണം
1914-ൽ രണ്ടു ജർമ്മൻ ശാസ്ത്രജ്ഞർ രസകരമായ ഒരു ഗവേഷണ പേപ്പർ പ്രസിദ്ധീകരിച്ചു. ആറ്റങ്ങളെ ചെറിയ കണങ്ങൾ കൊണ്ട് ഇടിച്ചാൽ എന്തു സംഭവിക്കുമെന്നതായിരുന്നു അവരുടെ പരീക്ഷണം. ജെയിംസ് ഫ്രാങ്ക് (James Franck, 1882-1964), ഗുസ്താഫ് ഹെർട്സ് (Gustaf Hertz, 1887-1975) എന്നിവർ ബെർലിൻ സർവ്വകലാശാലയിലാണ് ഈ പരീക്ഷണം നടത്തിയത്. രസത്തിൻ്റെ (മെർക്കുറി) യുടെ ആറ്റങ്ങളെ ഇലക്ട്രോണുകളെക്കൊണ്ട് ഇടിപ്പിക്കലായിരുന്നു പരീക്ഷണം. ഒരു ഫിലമെൻ്റ് ചൂടാക്കിയാണ് അവർ സ്വതന്ത്ര ഇലക്ട്രോണുകളെ ഉത്പാദിപ്പിച്ചത്. അതിനു ശേഷം ഒരു ഇലക്ടിക് പൊട്ടെൻഷ്യൽ ഉപയോഗിച്ച് അവയെ ആക്സിലറേറ്റ് ചെയ്യിച്ചു. വളരെ താഴ്ന്ന മർദ്ദത്തിലുള്ള മെർക്കുറി ആറ്റങ്ങളിൽ ഈ ഇലക്ട്രോണുകളെ പതിപ്പിച്ചു.
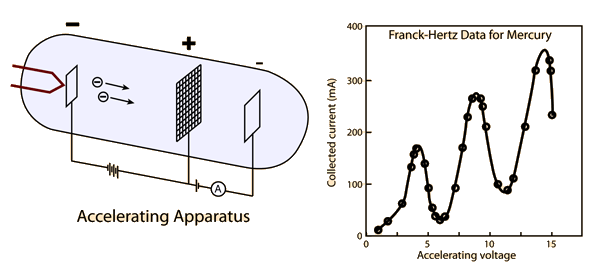
പരീക്ഷണത്തിൽ ആദ്യം ചെറിയ വോർട്ടേജ് മാത്രം നൽകിയപ്പോൾ ഇലക്ട്രോണുകൾ ഒഴുകുന്ന നിരക്ക് (കറൻ്റ്) വോർട്ടേജനുസരിച്ച് കൂടിക്കൊണ്ടിരുന്നു. എന്നാൽ വോൾട്ടേജ് 4.9 വോൾട്ട് കടന്നപ്പോൾ വൈദ്യുതിയുടെ നിരക്ക് ഏതാണ്ട് പൂജ്യത്തിലേക്ക് കൂപ്പുകുത്തി. അതായത് സെക്കൻഡിൽ 1300 കിലോമീറ്റർ എന്ന സ്പീഡിൽ നിന്ന് ഇലക്ട്രോണുകളുടെ വേഗം പെട്ടെന്ന് പൂജ്യമാവുകയായിരുന്നു. പിന്നെയും വോൾട്ടേജ് ഉയർത്തിയാൽ കറൻ്റ് കൂടും. എന്നാൽ വോൾട്ടേജ് എപ്പോഴൊക്കെ (4.9 V)-ൻ്റെ ഗുണിതങ്ങളാകുന്നുവോ അപ്പോഴൊക്കെ കറൻ്റ് പെട്ടെന്നു താഴും. ഇതായിരുന്നു അവരുടെ കണ്ടെത്തൽ. എന്നാൽ അവർക്ക് ഇതിൻ്റെ യഥാർത്ഥ കാരണം ഉടനെ നൽകാൻ കഴിഞ്ഞില്ല. സത്യത്തിൽ 1913-ൽ നീൽസ് ബോർ പ്രസിദ്ധീകരിച്ച സിദ്ധാന്തം അനുസരിച്ച് ഇതു വിശദീകരിക്കാൻ കഴിയുമായിരുന്നു. എന്നാൽ ഫ്രാങ്കും ഹെർട്സും നീൽസ് ബോറിൻ്റെ സിദ്ധാന്തത്തെക്കുറിച്ച് മനസ്സിലാക്കിയിരുന്നില്ല.
നീൽസ് ബോർ തന്നെയാണ് ഫ്രാങ്ക്- ഹെർട്സ് പരീക്ഷണത്തിന് ശരിയായ വിശദീകരണം നൽകിയത്. അത് ഇപ്രകാരമായിരുന്നു: മെർക്കുറി ആറ്റങ്ങൾക്ക് നിശ്ചിതമായ ഊർജനിലകളുണ്ട്. അതിൽ രണ്ട് നിലകൾ തമ്മിലുള്ള ഊർജവ്യത്യാസമാണ് 4.9 ഇലക്ട്രോൺ വോൾട്ട്, അതായത് ഒരു ഇലക്ട്രോണിനെ 4.9 വോൾട്ടിലൂടെ കടത്തിവിടുമ്പോൾ അതിനു ലഭിക്കുന്ന ഗതികോർജം അഥവാ കൈനെറ്റിക് എനെർജി. ഈ ഊർജം സ്വീകരിച്ച് ഒരു മെർക്കുറി ആറ്റം ഒരു ഊർജനിലയിൽ നിന്നും മറ്റൊരു ഊർജനിലയിലേക്കു നീങ്ങുന്നു. ഊർജം 4.9 eV-യുടെ ഇരട്ടിയായ 9.8 eV ആകുമ്പോൾ അത് രണ്ട് ആറ്റങ്ങളെ ഉയർന്ന നിലയിൽ എത്തിക്കാനുള്ള ഊർജമാകുമല്ലോ?
പിന്നീട് അവർ തന്നെ മറ്റൊരു ചോദ്യം ചോദിച്ചു; ഇലക്ട്രോണുകളുടെ ഇടി വഴി ലഭിച്ച ഊർജം കൊണ്ട് ഉയർന്ന നിലയിലേക്കു പോയ ആറ്റത്തിന് പ്രകാശരൂപത്തിൽ ആ ഊർജത്തെ പുറത്തുവിടാൻ കഴിയില്ലേ. 4.9 eV ഊർജമുള്ള പ്രകാശത്തിൻ്റെ തരംഗദൈർഘ്യം നമുക്കൊന്നു കണക്കാക്കാം (ഇവിടെ (1 eV= 1.602\times 10^{-19}J) എന്നത് ഓർക്കുക);
\begin{equation}
4.9 eV=E=h\nu=\frac{hc}{\lambda}
\end{equation}
അതായത്,
\begin{equation}
\lambda=\frac{hc}{E}=\frac{(6.626\times 10^{-34})( 2.998\times 10^8)}{4.9\times 1.602\times 10^{-19}}m
\end{equation}
ഇത് ഒരു കാൽക്കുലേറ്റർ ഉപയോഗിച്ച് കണക്കുകൂട്ടി നോക്കിയാൽ (\lambda=253) നാനോമീറ്റർ എന്നു കിട്ടും. ഇത് അൾട്രാവയലറ്റ് പ്രകാശമായിരിക്കും. അവർ തന്നെ തുടർന്നു നടത്തിയ പരീക്ഷണങ്ങളിൽ ഇലക്ട്രോണുകളുടെ ഇടി ഏറ്റുവാങ്ങുന്ന മെർക്കുറി ആറ്റങ്ങൾ ഇതേ തരംഗദൈർഘ്യമുള്ള അൾട്രാവയലറ്റ് പ്രകാശം പുറത്തുവിടുന്നുണ്ടെന്ന് മനസ്സിലാക്കി. ഇത് നീൽസ് ബോറിൻ്റെ ആറ്റം മാതൃകയ്ക്ക് പിന്തുണ നൽകിയ ഒരു ഒന്നാന്തരം പരീക്ഷണഫലം ആയിരുന്നു.
ഈ ഗവേഷണ പ്രവർത്തനങ്ങളുടെ പേരിൽ ഫ്രാങ്കിനും ഹെർട്സിനും 1925-ലെ ഫിസിക്സ് നോബെൽ പുരസ്കാരം ലഭിച്ചു.
5.2 സീമൻ ഇഫെക്റ്റ്

ക്വാണ്ടം സിദ്ധാന്തത്തിൻ്റെ വളർച്ചയിൽ സഹായിച്ച രണ്ടു പ്രഭാവങ്ങളെ സംബന്ധിച്ച് നമുക്ക് ഇവിടെ ചർച്ച ചെയ്യാം. ഇവയിൽ ആദ്യം കണ്ടെത്തിയതും കൂടുതൽ പ്രയോജനപ്പെട്ടതും സീമൻ പ്രഭാവം (Zeeman effect) തന്നെ. ഡച്ചുശാസ്ത്രജ്ഞനായ പീറ്റർ സീമൻ (Pieter Zeeman) ആണ് 1896-ൽ ഇതു പരീക്ഷണങ്ങളിലൂടെ കണ്ടെത്തിയത്. പ്രകാശ സ്രോതസ്സുകൾ ഉയർന്ന മാഗ്നെറ്റിക് ഫീൽഡിൽ (കാന്തികക്ഷേത്രത്തിൽ) ആയിരിക്കുമ്പോൾ അതിൻ്റെ സ്പെക്ട്രൽ രേഖകൾ പലതായി വിഭജിക്കപ്പെടും എന്നതായിരുന്നു സീമൻ്റെ കണ്ടെത്തൽ. ഉദാഹരണമായി സോഡിയം ആറ്റങ്ങളുടെ സ്പെക്ട്രത്തിൽ മഞ്ഞനിറത്തിലുള്ള രണ്ടു ലൈനുകൾ ഉണ്ട്. എന്നാൽ സോഡിയം ഒരു കാന്തികക്ഷേത്രത്തിൽ സ്ഥിതി ചെയ്യുകയാണെങ്കിൽ ഇവ ഓരോന്നും പലതായി പിളരും. ഇതാണ് സീമൻ ഇഫെക്റ്റ്.
സീമൻ ഈ പ്രഭാവം ആദ്യമായി കണ്ടെത്തുന്നത് 1896 -ലാണ്. അധികം താമസിയാതെ തന്നെ സീമൻ്റെ അദ്ധ്യാപകൻ കൂടിയായ ഹെൻഡ്രിക് ലോറെൻ്റ്സ് (Hendrik Lorentz) വികസിപ്പിച്ചെടുത്ത ഇലക്ട്രോൺ സിദ്ധാന്തം ഉപയോഗിച്ച് ഇതു വിശദീകരിക്കാൻ കഴിഞ്ഞു. ഈ ഗവേഷണങ്ങളുടെ പേരിൽ ഗുരുവും ശിഷ്യനും 1902-ലെ ഫിസിക്സ് നോബെൽ പുരസ്കാരം പങ്കിട്ടു.
ആദ്യകാലത്തെ ലോറെൻ്റ്സിൻ്റെ വിശദീകരണം ഇക്കാര്യത്തിൽ അവസാനവാക്കായിരുന്നില്ല. ഇലക്ട്രോണിൻ്റെ സ്പിൻ എന്ന സംഗതിയെക്കുറിച്ച് അന്ന് അറിയില്ലായിരുന്നു. ക്വാണ്ടം മെക്കാനിക്സ് വികസിച്ചതിനു ശേഷമാണ് സീമൻ ഇഫെക്റ്റ് തൃപ്തികരമായി വിശദീകരിക്കാൻ കഴിഞ്ഞത്.



5.3 സ്റ്റാർക്ക് ഇഫെക്റ്റ്
പ്രകാശ സ്രോതസ്സിലുള്ള ഇലെക്ടിക് ഫീൽഡ് (വൈദ്യുത ക്ഷേത്രം) മൂലം സ്പെക്ട്രൽ ലൈനുകൾ വിഭജിക്കപ്പെടുന്നതാണ് സ്റ്റാർക്ക് ഇഫെക്റ്റ്. സീമൻ ഇഫെക്റ്റും മാഗ്നെറ്റിക് ഫീൽഡും തമ്മിലുള്ള ബന്ധത്തിന് സമാനമാണ് സ്റ്റാർക്ക് ഇഫെക്റ്റും ഇലക്ടിക് ഫീൽഡുമായുള്ള ബന്ധം.

1913-ൽ ജർമ്മൻ ശാസ്ത്രജ്ഞനായ യൊഹാന്നെസ് സ്റ്റാർക് (Johannes Stark) ആണ് ഇത് കണ്ടെത്തിയത്. ഇതിൻ്റെ കൂടി പേരിൽ അദ്ദേഹത്തിന് 1919 -ലെ നോബെൽ പുരസ്കാരം ലഭിക്കുകയുമുണ്ടായി. ഹൈഡ്രജൻ്റെ കാര്യത്തിലാണ് ഈ പ്രഭാവം ആദ്യം കണ്ടെത്തിയത് പിന്നീട് മറ്റു പലവാതകങ്ങളുടെ കാര്യത്തിലും കണ്ടെത്തി. 100,000 V/cm എന്ന തീവ്രതയിലുള്ള ഇലക്ട്രിക് ഫീൽഡ് സൃഷ്ടിക്കുക വഴിയാണ് ഇതു സാധിച്ചത്. സീമൻ ഇഫെക്റ്റു പോലെ ഇതും ക്വാണ്ടം തിയറിയുടെ വളർച്ചയെ സഹായിച്ചിട്ടുണ്ട്. അടുത്ത സെക്ഷനിൽ വിവരിക്കുന്ന ബോർ സമെർഫെൽഡ് മോഡെലനുസരിച്ച് ഇതു വിശദീകരിക്കാൻ കഴിയും. എങ്കിലും ഇതിനു കൃത്യത വരുന്നത് ക്വാണ്ടം മെക്കാനിക്സിലൂടെയാണ്. ഏതായാലും ക്ലാസ്സിക്കൽ ഭൗതികം മാത്രം ഉപയോഗിച്ചു കൊണ്ട് ഇതിൻ്റെ വിശദീകരണം സാദ്ധ്യമല്ല.
5.4 ബോർ-സമെർഫെൽഡ് മാതൃക
നീൽസ് ബോറിന്റെ ആറ്റം മാതൃകയിൽ ചില പരിഷ്കാരങ്ങൾ വരുത്തി ആർനോൾഡ് സമർഫെൽഡ് എന്ന ജർമ്മൻ ശാസ്ത്രജ്ഞൻ അവതരിപ്പിച്ച സിദ്ധാന്തമാണ് ഈ പേരിൽ അറിയപ്പെടുന്നത്. പിന്നീട് ക്വാണ്ടം മെക്കാനിക്സ് നിലവിൽ വന്നതോടെ ഇതിന് പ്രസക്തി നഷ്ടപ്പെട്ടെങ്കിലും ക്വാണ്ടം സിദ്ധാന്തത്തിൻ്റെ ചരിത്രത്തിൽ ഇതിന് ഒരു സ്ഥാനമുണ്ട്.
എന്നാൽ സമർഫെൽഡിന്റെ ഏറ്റവും വലിയ സംഭാവനയായി ശാസ്ത്രലോകം കരുതുന്നത് അദ്ദേഹം ഏറെ വിദ്യാർത്ഥികളെ മിടുക്കരാക്കി വളർത്തിയെടുത്തു എന്നതാണ്. വെർണർ ഹൈസെൻബെർഗ്, വുൾഫ്ഗാങ് പൗളി, ഹാൻസ് ബെഥെ, പീറ്റർ ഡെബെ എന്നിവർ ഉൾപ്പടെ അദ്ദേഹത്തിൻ്റ മേൽനോട്ടത്തിൽ. ഗവേഷണം നടത്തിയ ഏഴു വിദ്യാർത്ഥികൾ നോബെൽ പുരസ്കാരം നേടിയിട്ടുണ്ട്. 84 തവണ നോബെൽ പുരസ്കാരത്തിന് നോമിനേറ്റു ചെയ്യപ്പെട്ടെങ്കിലും അദ്ദേഹത്തിന് അത് ഒരിക്കലും ലഭിച്ചില്ല.

നീൽസ് ബോറിന്റെ ആറ്റംമാതൃകയിൽ ഇലക്ട്രോണുകൾ ന്യൂക്ലിയസിനു ചുറ്റും വൃത്താകാര ഭ്രമണപഥത്തിൽ തിരിയുന്നു. എന്നാൽ സമെർഫെൽഡിന്റെ പരിഷ്കാരത്തിൽ ഭ്രമണപഥങ്ങൾ ദീർഘവൃത്തങ്ങൾ (ellipses) ആകാം. സൗരയൂഥത്തിൻ്റെ കാര്യമെടുത്താൽ, ഗ്രഹങ്ങൾ സഞ്ചരിക്കുന്നത് കൃത്യമായ വൃത്തപഥത്തിലല്ല, മറിച്ച് ദീർഘവൃത്തത്തിലാണെന്ന് കെപ്ളെർ കണ്ടെത്തുകയും ഐസക്ക് ന്യൂട്ടൺ തൻ്റെ ഗുരുത്വാകർഷണസിദ്ധാന്തത്തിൻ്റെ അടിസ്ഥാനത്തിൽ വിശദീകരിക്കുകയും ചെയ്തിരുന്നു. അവിടെ അതിനു കാരണമായി പറയുന്നത് രണ്ടു വസ്തുക്കൾ തമ്മിലുള്ള ഗുരുത്വാകർഷണമെന്നത് അവ തമ്മിലുള്ള ദൂരത്തിൻ്റെ വർഗത്തിന് വിപരീതാനുപാതത്തിലാണ് എന്നതാണ്. അത് ചാർജുകൾ തമ്മിലുള്ള കൂളോം ബലത്തിൻ്റെ (Coulomb force) കാര്യത്തിലും ശരിയാണ്. ഇതേ തത്വം ഉപയോഗിച്ചാണ് ന്യൂക്ലിയസിനു ചുറ്റുമുള്ള ഇലക്ട്രോണിൻ്റെ ഭ്രമണപഥം ദീർഘവൃത്തവും ആകാമെന്ന ആശയം അവതരിപ്പിച്ചത്.
ക്വാണ്ടം നമ്പർ എന്ന ആശയവും ആദ്യമായി അവതരിപ്പിച്ചത് സമെർഫെൽഡാണ്. ബോർ ആറ്റം മോഡെലിലെ ഊർജനിലകളുടെ സമവാക്യത്തിലെ (n) എന്നത് പ്രിൻസിപ്പൽ ക്വാണ്ടം നമ്പർ.
\begin{equation}
n=1,2,3,…
\end{equation}
ഓരോ (n)-നും ഒരേ ഊർജനിലയിലുള്ള, അതേ സമയം വ്യത്യസ്തമായ ഉൽകേന്ദ്രത (eccentrcity) ഉള്ള (n) ഭ്രമണപഥങ്ങൾ ഉണ്ടായിരിക്കും. അവയെ സൂചിപ്പിക്കാൻ (l) എന്ന ക്വാണ്ടം നമ്പർ ഉപയോഗിക്കുന്നു. (l)-ൻ്റെ മൂല്യം,
\begin{equation}
l=0, 1, 2,3, …, n-1.
\end{equation}
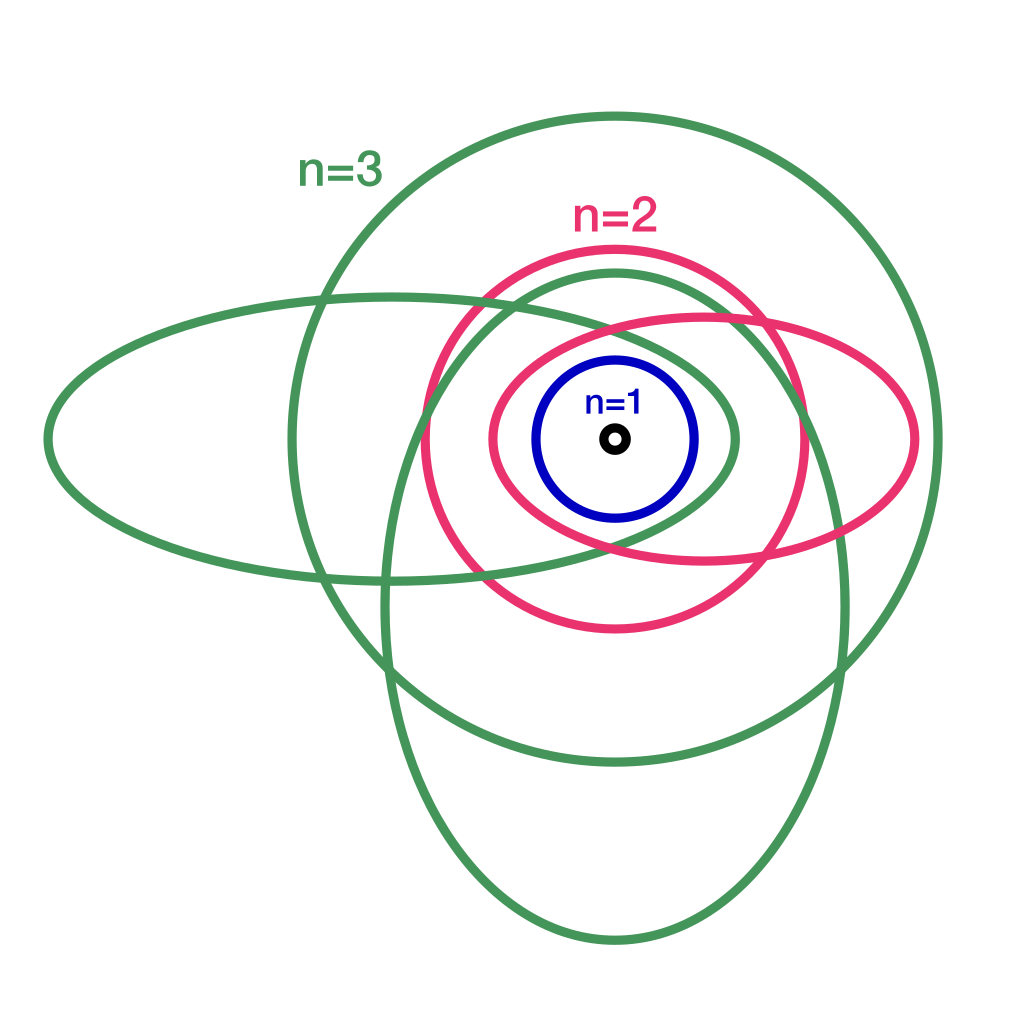
അടുത്തതായി പറയേണ്ടത് മാഗ്നറ്റിക് ക്വാണ്ടം നമ്പർ ((m_l)) എന്നറിയപ്പെടുന്ന സംഗതിയെക്കുറിച്ചാണ്. കാന്തികമണ്ഡലത്തിൽ സംഭവിക്കുന്ന സീമൻ പ്രഭാവത്തെ വിശദീകരിക്കാൻ ഇതു പ്രയോജനപ്പെടുത്തുന്നു. ഇതിൻ്റെ മൂല്യം (+l) മുതൽ (-l) വരെയാകാം,
\begin{equation}
m_l=l,l-1,l-2,…,-l
\end{equation}
ഒരു സാധാരണ സ്പെക്ട്രോമീറ്ററിലൂടെ ഹൈഡ്രജൻ സ്പെക്ട്രം കാണുമ്പോൾ നീൽസ് ബോറിൻ്റെ ആറ്റം മോഡെൽ വിശദീകരിക്കുന്ന രീതിയിലുള്ള രേഖകൾ തന്നെയാണ് കാണുക. എന്നാൽ സൂക്ഷ്മത കൂടിയ മുന്തിയ ഇനം സ്പെക്ട്രോമീറ്ററുകൾ ഉപയോഗിച്ചു പരിശോധിച്ചാൽ ഈ ലൈനുകൾ അടുത്തടുത്ത ഒന്നിലധികം നേർത്ത വരകൾ ചേർന്നതാണെന്നു മനസ്സിലാക്കാം. ഇതിനെയാണ് സൂക്ഷ്മ ഘടന (fine structure) എന്നു വിളിക്കുന്നത്. ഇതു സംബന്ധിച്ച് അന്നു ലഭ്യമായിരുന്ന പരീക്ഷണഫലങ്ങളെ വിശദീകരിക്കാൻ സമെർഫെൽഡിനു കഴിഞ്ഞു. ഹൈഡ്രജൻ ആറ്റത്തിൽ ഇലക്ട്രോണുകൾ സാമാന്യം നല്ല വേഗത്തിലാണ് സഞ്ചരിക്കുന്നതെന്നും അതിനാൽ ഐൻസ്റ്റൈൻ്റെ ആപേക്ഷികതാ
സിദ്ധാന്തവുമായി യോജിക്കുന്ന തരത്തിൽ സമവാക്യങ്ങൾ മാറ്റണമെന്നും അദ്ദേഹം കരുതി. ആ രീതിയിൽ കണക്കുകൂട്ടിയപ്പോൾ ദീർഘവൃത്താകൃതിയിലുള്ള പഥത്തിലൂടെ സഞ്ചരിക്കുന്ന ഇലക്ട്രോണുകളുടെ ഊർജത്തിൽ ഉണ്ടാകുന്ന ചെറിയ മാറ്റത്തിന് ഒരു ഫോർമുല അദ്ദേഹം കണ്ടെത്തി. അതു പരീക്ഷണങ്ങളുമായി തട്ടിച്ചു നോക്കിയപ്പോൾ തൃപ്തികരമായിരുന്നു.
ക്വാണ്ടം കോഴ്സിന്റെ ഭാഗമായി ഇതുവരെ പങ്കിട്ട കുറിപ്പുകൾ
