6.1 സ്റ്റേൺ-ഗെർലാക് പരീക്ഷണം
ക്വാണ്ടം തിയറിയുടെ ചരിത്രത്തിലെ രസകരമായ ഒരു സംഭവമായിരുന്നു രണ്ടു ജർമ്മൻ ശാസ്ത്രജ്ഞർ നടത്തിയ ഈ പരീക്ഷണം. ഒരിക്കൽ ഐൻസ്റ്റൈൻ്റെ ശിഷ്യനായിരുന്ന ഓട്ടോ സ്റ്റേൺ (Otto Stern) തൻ്റെ ഒരു ആശയം വാൾതെർ ഗെർലാക് (Walther Gerlach) എന്ന ശാസ്ത്രജ്ഞനോടൊപ്പം 1922-ൽ പരീക്ഷിച്ചു നോക്കുകയായിരുന്നു. അന്ന് പ്രചാരത്തിലിരുന്ന ബോർ- സോമെർഫെൽഡ് മോഡെൽ അനുസരിച്ച് ഇലക്ട്രോൺ ന്യൂക്ലിയസിനുചുറ്റും വലിയ വേഗത്തിൽ കറങ്ങിക്കൊണ്ടിരിക്കുന്നു. ചാർജുള്ള ഒരു കണം ചുറ്റിസഞ്ചരിക്കുന്നത് ഒരു സാങ്കല്പിക കോയിലിലൂടെ കറൻ്റ് പ്രവഹിക്കുന്നതിനു സമാനമാണ്. അത് മാഗ്നെറ്റിക് ഫീൽഡിനു കാരണമാകും. (e) ചാർജും (m) മാസുമുള്ള ഇലക്ട്രോൺ (\frac{h}{2\pi}) കോണീയ സംവേഗത്തോടെ കറങ്ങുമ്പോൾ അതിനൊരു മാഗ്നെറ്റിക് മൊമെൻ്റ് (ഇതിന് ബാർ മാഗ്നെറ്റോൺ, (\mu_B) എന്നാണ് പേര്) ഉണ്ടാകും, അതിൻ്റെ മൂല്യം,
\begin{equation}
\mu_B=\frac{e}{2m}\frac{h}{2\pi}.
\end{equation}
അതായത്, ആ ആറ്റം ഒരു ചെറുകാന്തത്തിൻ്റെ സ്വഭാവം കാണിക്കും. അതിൻ്റെ കാന്തികശേഷിയെ സൂചിപ്പിക്കുന്ന മാഗ്നെറ്റിക് മൊമെൻ്റ് എന്നത് കോണീയ സംവേഗത്തിന് (angular momentum) ആനുപാതികമായിരിക്കും. ഈ വെക്ടറിൻ്റെ ഒരു ദിശയിലുള്ള കമ്പോണെൻ്റിന് നിശ്ചിത മൂല്യങ്ങൾ മാത്രമേ എടുക്കാൻ കഴിയൂ എന്നത് ബോർ- സോമെർഫീൽഡ് മോഡെലിൻ്റെ ഒരു അനുമാനമായിരുന്നു. ഇതു സ്പേസ് ക്വാണ്ടൈസേഷൻ എന്നറിയപ്പെട്ടിരുന്നു. ഇതിനെ സംബന്ധിച്ച് സംശയാലുവായിരുന്ന ഓട്ടോ സ്റ്റേൺ ഇതു പരിശോധിക്കാൻ ഒരു പരീക്ഷണം രൂപകല്പന ചെയ്തു.
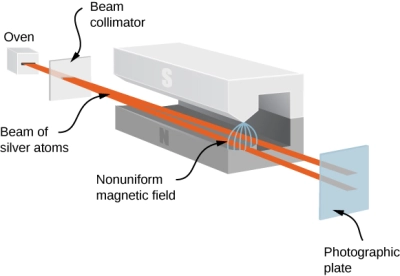
കുറേ ആറ്റങ്ങളെ സാമാന്യം വേഗത്തിൽ ഏകസമാനമല്ലാത്ത (nonuniform) ശക്തമായ ഒരു മാഗ്നെറ്റിക് ഫീൽഡിലൂടെ കടത്തി വിടുക എന്നതായിരുന്നു ആശയം. ക്ലാസ്സിക്കൽ ധാരണകളനുസരിച്ചാണെങ്കിൽ കാന്തികക്ഷേത്രത്തിലൂടെ കടന്നുപോകുമ്പോൾ ആറ്റങ്ങളുടെ ബീം കുറച്ച് സ്പ്രെഡ് ചെയ്യും. എന്നാൽ കേന്ദ്രഭാഗത്തായിരിക്കും ഏറ്റവും കൂടുതൽ. അതേ സമയം സമെർഫെൽഡിൻ്റെ ക്വാണ്ടൈസേഷൽൻ തത്വങ്ങൾ അനുസരിച്ചാണെങ്കിൽ കാന്തങ്ങൾക്ക് ചില പ്രത്യേക ഓറിയൻ്റേഷനുകൾ മാത്രമേ എടുക്കാൻ കഴിയൂ എന്നതിനാൽ ബീം വിഭജിക്കപ്പെടും. ഇവർ പരീക്ഷണത്തിൽ സിൽവർ ആറ്റങ്ങളെയാണ് ഉപയോഗിച്ചത് പരീക്ഷണങ്ങൾക്കൊടുവിൽ സിൽവർ ആറ്റങ്ങളുടെ ബീം രണ്ടായി വിഭജിക്കപ്പെട്ടാണ് സ്ക്രീനിൽ പതിഞ്ഞത്. ഇത് ബോർ-സമർ ഫെൽഡ് മോഡെലിന് വലിയ പിന്തുണ നൽകി.

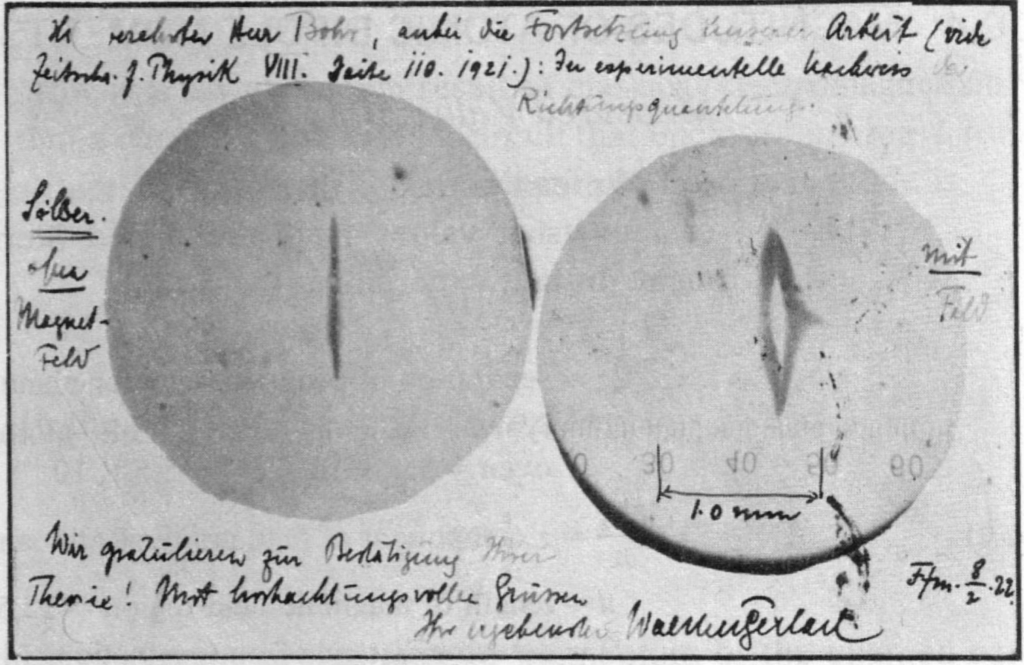
സ്റ്റേൺ ഗെർലാക് പരീക്ഷണവുമായി ബന്ധപ്പെട്ട സംഭവപരമ്പരയിൽ പല ട്വിസ്റ്റുകളും ഉണ്ടായിട്ടുണ്ട്. ഒന്നാമതായി, ബോർ -സമെർഫെൽഡ് മാതൃക ശരിയല്ലെന്നും ഇത്തരത്തിൽ ഒരു പ്രഭാവം ഉണ്ടാകില്ലെന്നുമാണ് തുടക്കത്തിൽ സ്റ്റേൺ കരുതിയിരുന്നത്. പക്ഷേ, അദ്ദേഹത്തിൻ്റെ തന്നെ പ്രതീക്ഷക്കു വിരുദ്ധമായ പരീക്ഷണഫലമാണു ലഭിച്ചത്. “നീൽസ് ബോറിൻ്റെ ഈ നോൺസെൻസ് ശരിയാണെന്ന് തെളിഞ്ഞാൽ, നമ്മൾ ഫിസിക്സ് വിടും” എന്നൊക്കെ ഒരിക്കൽ പറഞ്ഞ ആളായിരുന്നു സ്റ്റേൺ. ഒടുവിൽ, ഇതു തെളിയിച്ചതിൻ്റെ പേരിലാണ് ഇദ്ദേഹത്തിന് നോബെൽ പുരസ്കാരം ഉൾപ്പെടെയുള്ള ബഹുമതികൾ ലഭിച്ചത്. രണ്ടാമത്തെ ട്വിസ്റ്റ് സ്റ്റേണിന് ഉണ്ടായിരുന്ന ഒരു ദുഃസ്വഭാവം ഈ പരീക്ഷണത്തിൽ വലിയ തുണയായ സംഭവമാണ്. ഈ പരീക്ഷണത്തിൽ സിൽവെർ ആറ്റങ്ങൾക്ക് ചലനസ്വാതന്ത്ര്യം കിട്ടാൻ വേണ്ടി പരീക്ഷണത്തിനായി ചേമ്പറിനുള്ളിൽ ശൂന്യത സൃഷ്ടിച്ചിരുന്നു. പിന്നീട് വായു കടത്തിവിട്ടതിനു ശേഷം ചേമ്പർ തുറന്ന് സിൽവെർ ആറ്റങ്ങൾ വീണ പ്ലേറ്റ് പരിശോധിച്ചു. നോക്കിയപ്പോൾ ആദ്യം അതിൽ ഒന്നും തന്നെ കാണുന്നുണ്ടായിരുന്നില്ല. പിന്നീട്, രണ്ടു കറുത്ത രേഖകൾ തെളിഞ്ഞു വന്നു. ആത് വലിയ അത്ഭുതമായി, പിന്നീടാണ് കാര്യങ്ങൾ വ്യക്തമായത്. അന്ന് സ്റ്റേണിന് ചുരുട്ട് (സിഗാർ) വലിക്കുന്ന സ്വഭാവം ഉണ്ടായിരുന്നു. ശമ്പളം കുറവായിരുന്നതിനാൽ, വിലകുറഞ്ഞ സിഗാറുകളാണ് അയാൾ വലിച്ചിരുന്നത്. അതിൽ സൾഫറിൻ്റെ അളവ് കൂടുതലായിരുന്നു. സ്റ്റേണിൻ്റെ നിശ്വാസവായു വീണ് പ്ലേറ്റിൽ സിൽവർ സർഫൈഡ് ഉണ്ടായതാണ് കറുത്ത വരകളായി തെളിഞ്ഞു വന്നത്! ഒരു പക്ഷേ പുകയും സഹായിച്ചിട്ടുണ്ടാകും.
ഇനിയും മറ്റൊരു ട്വിസ്റ്റ് കൂടി ഇതിലുണ്ട്. ഈ പരീക്ഷണം നടക്കുന്ന 1922-ൽ ഇലക്ട്രോണിൻ്റെ സ്പിൻ എന്നൊരു സംഗതിയെക്കുറിച്ച് ശാസ്ത്രലോകത്തിന് അറിവുണ്ടായിരുന്നില്ല. പിന്നീട് 1925-ലാണ് അതിനെക്കുറിച്ചു വ്യക്തത വരുന്നത്. അതോടെ മനസ്സിലായത് സ്റ്റേൺ- ഗെർലാക് പരീക്ഷണത്തിൽ ബീമിനെ പിിളർത്തിയത് ഇലക്ട്രോണിൻ്റെ സ്പിൻ ആണെന്നതാണ്.സിൽവെർ ആറ്റങ്ങളുടെ ഇലക്ട്രോണിക് ഘടന (1s^22s^2p^63s^2p^6d^{10}4s^2p^6d^{10}5s^1) എന്നതാണ്. ഇതിലെ ജോടിയാവാത്ത ഒടുവിലത്തെ ഇലക്ട്രോൺ (s) സ്റ്റേറ്റിൽ ആയതിനാൽ അതിന് ഓർബിറ്റൽ ആൻഗുലാർ മൊമെൻ്റം ഉണ്ടാവില്ല. പക്ഷേ, സ്പിൻ ഉണ്ടാകും. എന്നാൽ ഇക്കാര്യമൊന്നും 1922-ൽ അറിഞ്ഞിരുന്നില്ല.
6.2 സ്പിൻ എന്ന പ്രഹേളിക
ആദ്യംതന്നെ ഒരു കാര്യം പറയട്ടെ. `സ്പിൻ ആൻഗുലാർ മൊമെൻ്റം’ എന്നതിൻ്റെ ചുരുക്കപ്പേരായാണ് സ്പിൻ എന്ന വാക്ക് ക്വാണ്ടം മെക്കാനിക്സിൽ ഉപയോഗിക്കുന്നത്. ഇലക്ട്രോൺ, പ്രോട്ടോൺ, ന്യൂട്രോൺ, ഫോട്ടോൺ ഇത്യാദിയായ, നമുക്കു പരിചിതമായ ധാരാളം കണങ്ങൾക്ക് സ്പിൻ ഉണ്ട്. ഇത് ഒരു ക്വാണ്ടം സംഗതിയാണ്. നമുക്കു ക്ലാസ്സിക്കൽ ഭൗതികത്തിലൂടെ പരിചിതമായ എന്തെങ്കിലും കാര്യങ്ങളുമായി ഇതിനെ സമീകരിക്കാൻ ശ്രമിച്ചാൽ വിജയിക്കില്ല.
നെതർലൻഡ്സിലെ ലൈഡെൻ സർവ്വകലാശാലയിൽ എറെൻഫെസ്റ്റ് എന്ന ശാസ്ത്രജ്ഞൻ്റെ മേൽനോട്ടത്തിൽ ഗവേഷണം നടത്തിയിരുന്ന ജോർജ് ഊലെൻബെക്ക് (George Uhlenbeck), സാമുവെൽ ഗോഡ്സ്മിറ്റ് (Samuel Goudsmit) എന്നിവരാണ് ഇലക്ട്രോണിന് സ്പിൻ ആൻഗുലാർ മൊമെൻ്റം ഉണ്ടെന്ന ആശയം 1925-ൽ അവതരിപ്പിച്ചത്. ഓരോ ഇലക്ട്രോണും സ്വയം തിരിയുന്നുവെന്നും അതിൻ്റെ ആംഗുലാർ മൊമെൻ്റം (\frac{1}{2}\left(\frac{h}{2\pi}\right)=\frac{1}{2}\hbar) ആണെന്നുമായിരുന്നു അവരുടെ സിദ്ധാന്തം.

1925-ൽ ഇവർ ഇരുവരും ഈ `തലതിരിഞ്ഞ’ ആശയവുമായി എറെൻഫെസ്റ്റിനെ സമീപിച്ചു. ഐഡിയ കൊള്ളാമല്ലോ എന്നു പറഞ്ഞ് അവരെ പ്രോത്സാഹിപ്പിച്ച അദ്ദേഹം അവരോട് അത് പ്രസിദ്ധീകരിക്കാനായി ഒരു കുറിപ്പാക്കാൻ പറഞ്ഞു. അതിനിടയിൽ, ഈ വിഷയത്തിൽ വിദഗ്ധനായ ലോറെൻ്റ്സിനോട് തൻ്റെ വിദ്യാർത്ഥികൾക്ക് അവരുടെ ഈ രസികൻ ആശയം ചർച്ച ചെയ്യാൻ അപ്പോയ്ൻ്റ്മെൻ്റ് ചോദിച്ചു കൊണ്ട് കത്തെഴുതുകയും ചെയ്തു. ഇലക്ട്രോണിന് സ്വയം തിരിയാൻ ക്ലാസ്സിക്കൽ ഇലക്ട്രോഡൈനാമിക്സ് അനുവദിക്കുന്നില്ലെന്നു ലോറെൻ്റ്സ് വാദിച്ചു. ഇതോടെ, ഊലെൻബെക്ക് അവരുടെ കുറിപ്പ് പ്രസിദ്ധീകരണത്തിനയക്കണ്ട എന്ന് എറെൻഫെസ്റ്റിനോട് പറഞ്ഞു. അത് അയച്ചു കഴിഞ്ഞല്ലോ എന്നതായിരുന്നു എന്നതായിരുന്നു മറുപടി. “നിങ്ങൾ ചെറുപ്പമല്ലേ? കുറച്ചു വങ്കത്തരം ഒക്കെ ആകാം” എന്നു കൂടി എറെൻഫെസ്റ്റ് കൂട്ടിച്ചേർത്തു. ശേഷം, സംഭവിച്ച കാര്യങ്ങൾ നിമിത്തം ശാസ്ത്രചരിത്രം ഈ ആശയത്തെ ഒരു വഴിത്തിരിവായി രേഖപ്പെടുത്തുന്നു. പക്ഷേ, ഇരുവരുടേയും പേരുകൾ ഏതാണ്ട് അൻപതു തവണ നോബെൽ പുരസ്കാരത്തിനു നിർദ്ദേശിക്കപ്പെട്ടെങ്കിലും അവർക്കത് ഒരിക്കലും ലഭിച്ചില്ല.
സ്പിൻഎന്ന ആശയം അവതരിപ്പിക്കാൻ അവരെ പ്രേരിപ്പിച്ച ചില പ്രധാനപ്പെട്ട പരീക്ഷണഫലങ്ങൾ നമുക്കൊന്ന് പരിചയപ്പെടാം. പല വാതകങ്ങളുടെയും സ്പെക്ട്രം സൂക്ഷ്മമായ വിശകലനത്തിനു വിധേയമാക്കുമ്പോൾ ഒരു ലൈൻ ആണെന്നു നമ്മൾ ആദ്യം കരുതിയിരുന്നത് പലതാകും. ഉപകരണങ്ങളുടെ സൂക്ഷ്മത കുറേക്കൂടി വർദ്ധിപ്പിച്ചാൽ അതു തന്നെ വീണ്ടും പലതായി കാണും. ഈ അതിസൂക്ഷ്മ ഘടന (hyperfine structure) വിശദീകരിക്കാൻ (n, l, m_l) എന്നീ ക്വാണ്ടം നമ്പറുകൾ മതിയാകില്ല. അവിടെ, പുതുതായി സ്പിൻ ക്വാണ്ടം നമ്പർ (m_s) എന്ന ഒന്നുകൂടി ചേർത്താൽ കാര്യങ്ങൾ എളുപ്പമാകും. ഇതു കൂടാതെ ചില കേസുകളിലെ സീമൻ പ്രഭാവം ക്ലാസ്സിക്കൽ സിദ്ധാന്തങ്ങൾ കൊണ്ട് വിശദീകരിക്കാൻ കഴിയില്ല. അവയെ അനോമലസ് സീമൻ ഇഫെക്റ്റ് എന്നു വിളിക്കുന്നു. ഉദാഹരണമായി സോഡിയത്തിൻ്റെ കാര്യത്തിൽ സാധാരണ സ്പെക്ട്രം എടുത്താൽ അതിൽ അടുത്തടുത്തുള്ള രണ്ടു മഞ്ഞ വരകൾ കാണാം. ഇവയുടെ തരംഗദൈർഘ്യം നാനോമീറ്ററിൽ (589.0)-ഉം (589.6)-ഉം ആണ്. ശക്തിയുള്ള കാന്തികക്ഷേത്രവും നല്ല റെസൊലൂഷനും ഉള്ള സ്പെക്ട്രോമീറ്റർ ഉപയോഗിച്ച് പരിശോധിച്ചാൽ ഇതിൽ ആദ്യത്തേത് നാലായും രണ്ടാമത്തേത് ആറായും പിളർന്ന രീതിയിൽ കാണാം. ഇതു വിശദീകരിക്കാൻ സ്പിൻ ആവശ്യമാണ്. കൂടാതെ പൗളിയുടെ തത്വം (Pauli’s exclusion principle) ഉപയോഗിച്ച് ആറ്റംഘടന വിശദീകരിക്കാനും സ്പിൻ സഹായിക്കുന്നു.
ഈ സെക്ഷൻ അവസാനിപ്പിക്കുന്നതിനു മുമ്പേ ഒരു കാര്യം കൂടി കൂട്ടിച്ചേർത്തില്ലെങ്കിൽ നീതിയാവില്ല. 1925 ജനുവരിയിൽ ഗവേഷക വിദ്യാർത്ഥിയായിരുന്ന 20 വയസ്സുകാരൻ റാൽഫ് ക്രോണിഗ് (Ralf Kronig) എന്ന മിടുക്കൻ ഇലക്ട്രോണിൻ്റെ സ്പിൻ എന്ന ആശയം സ്വന്തമായി വികസിപ്പിച്ചെടുത്തിരുന്നു. എന്നാൽ, അയാൾ ഇതിനെ സംബന്ധിച്ച് വോൾഫ്ഗാങ് പോളിയോടു സംസാരിച്ചപ്പോൾ അദ്ദേഹം ഈ ആശയത്തെ തള്ളി. “കാഞ്ഞ ബുദ്ധി തന്നെ, പക്ഷേ, യാഥാർത്ഥ്യവുമായി ഒരു ബന്ധവുമില്ല” എന്ന പോളിയുടെ പരിഹാസവും കൂടി ആയപ്പോൾ ക്രോണിഗ് തൻ്റെ ആശയം പ്രസിദ്ധീകരിക്കേണ്ടെന്നു വച്ചു. പിന്നീട്, മാസങ്ങൾക്കു ശേഷമാണ് ഊലെൻബെക്കും ഗോഡ്സ്മിറ്റും ചേർന്നെഴുതിയ പേപ്പർ പ്രസിദ്ധമാകുന്നത്. ഇതൊക്കെ സംഭവിച്ചുവെങ്കിലും ക്രോണിഗും പോളിയും നല്ല സുഹൃത്തുക്കളായി തുടരുകയും ധാരാളം ആശയങ്ങൾ കത്തുകളിലൂടെ കൈമാറുകയും ചെയ്തു.
6.3 വോൾഫ്ഗാങ് പോളിയും പോളി തത്വവും
ക്വാണ്ടം മെക്കാനിക്സിൻ്റെ ഒരു പുസ്തകത്തിലും വിട്ടുകളയാൻ പറ്റാത്ത ഒരു മിടുക്കനായ രസികൻ ശാസ്ത്രജ്ഞനായിരുന്നു വോൾഫ്ഗാങ് പോളി (Wolfgang Pauli). 1900 ഏപ്രിൽ 25-ന് ആസ്ത്രിയയുടെ തലസ്ഥാനമായ വിയന്നയിൽ ജനിച്ച പോളിമിടുക്കനായ ഒരു വിദ്യാർത്ഥിയായിരുന്നു. തൻ്റെ 18-ാം വയസ്സിൽ റിലേറ്റിവിറ്റിയെ സംബന്ധിച്ച് ഒരു ഗവേഷണ പേപ്പർ പ്രസിദ്ധീകരിച്ച് ശാസ്ത്രജ്ഞരുടെ ശ്രദ്ധ പിടിച്ചു പറ്റിയ പോളി, 1921 ആയപ്പോഴേക്കും ഡോക്ടറേറ്റും നേടി. സമെർഫെൽഡായിരുന്നു ഗവേഷണ ഗൈഡ്. 1923-ൽ ഹാംബർഗ് സർവ്വകലാശാലയിൽ പ്രൊഫസ്സറായ പോളി ശ്രദ്ധേയമായ കണ്ടെത്തലുകൾ നടത്തി. 1945-ലെ ഫിസിക്സ് നോബെൽ പുരസ്കാരം പോളിക്കായിരുന്നു.
പോളിയുടെ ഗവേഷണനേട്ടങ്ങളിൽ പ്രധാനപ്പെട്ട ഒന്നായിരുന്നു പിന്നീട് പോളി എക്സ്ക്ലൂഷൻ പ്രിൻസിപ്പ്ൾ എന്നറിയപ്പെട്ട ഒഴിവാക്കൽ തത്വം. അതിലേക്കു നയിച്ച കാര്യങ്ങൾ ഒന്നു ചുരുക്കിപ്പറയാം.

പോളി തുടങ്ങിയത് ബോർ- സമെർഫെൽഡ് മോഡെലിൽ നിന്നായിരുന്നു. ഹൈഡ്രജൻ്റെ ഏറ്റവും കുറഞ്ഞ ഊർജനിലയിൽ ഇലക്ട്രോൺ സഞ്ചരിക്കുന്ന വൃത്തപാതയുടെ റേഡിയസിനുള്ള (ബോർ റേഡിയസ്) ഒരു സമവാക്യം (\ref{radius1}) നമ്മൾ മുമ്പ് ഉണ്ടാക്കിയെടുത്തിരുന്നല്ലോ. അതായത്,
\begin{equation}
r_1=\frac{h^2}{4\pi^2kme^2}
\end{equation}
അടുത്തതായി നമ്മൾ ഹൈഡ്രജനു പകരം (Z) അറ്റോമിക് നമ്പറുള്ള ഒരു ആറ്റത്തിൻ്റെ കാര്യം പരിഗണിക്കുക. അതിൻ്റെ ന്യൂക്ലിയസിൽ (Z) പ്രോട്ടോണുകൾ ഉണ്ടായിരിക്കും. അതിൻ്റെ ചുറ്റും ഒരൊറ്റ ഇലക്ട്രോൺ തിരിയുന്ന കാര്യമെടുത്താൽ അതു ചെലുത്തുന്ന ബലം (k\frac{Ze^2}{r^2}) ആയിരിക്കും. ഈ കേസിൽ, ബോർ റേഡിയസിനു പകരം നമുക്കു കിട്ടുക
\begin{equation}
R _{1}=\frac{h^2}{4\pi^2kmZe^2}
\end{equation}
എന്നായിരിക്കും. ഈ സമവാക്യത്തിൽ ഡിനോമിനേറ്ററിൽ (ഛേദം) (Z) ഉണ്ടെന്നതു ശ്രദ്ധിക്കുക. അതായത് അറ്റോമിക് നമ്പർ കൂടുന്നതനുസരിച്ച് റേഡിയസ് കുറഞ്ഞു വരണം. ഇവിടെ നമ്മൾ ഒരു ഇലക്ട്രോണിൻ്റെ കാര്യമാണ് പറഞ്ഞത്. യഥാർത്ഥത്തിൽ (Z) ഇലക്ട്രോണുകൾ ഉണ്ടാകുമല്ലോ. ഇവയെ എല്ലാം ഗ്രൗണ്ട് സ്റ്റേറ്റിലേക്ക് തന്നെ പറഞ്ഞയച്ചാൽ റേഡിയസ് ഈ അളവിൽ തന്നെ നില്ക്കും. പക്ഷേ, ഇത് പരീക്ഷണങ്ങളുമായി ചേർന്നു പോകുന്നുണ്ടായിരുന്നില്ല. അണുസംഖ്യ കൂടുമ്പോൾ റേഡിയസ് കുറഞ്ഞുവരുന്നില്ല.
അടുത്തതായി ഊർജത്തിൻ്റെ കാര്യം പരിഗണിക്കാം. ഒരു ന്യൂട്രൽ ആറ്റത്തിൽ നിന്ന് ഒരു ഇലക്ട്രോണിനെ വിടുതൽ ചെയ്യിക്കാൻ വേണ്ട മിനിമം ഊർജത്തെയാണ് അയണീകരണ ഊർജം അഥവാ അയോണൈസേഷൻ എനെർജി എന്നു വിളിക്കുന്നത്. ഹൈഡ്രജൻ ആറ്റത്തിൻ്റെ കാര്യത്തിൽ ഇത് (13.6 eV) ആണ്. മേൽ പറഞ്ഞ കാര്യങ്ങൾ ശരിയെങ്കിൽ അറ്റോമിക നമ്പർ കൂടിയ ആറ്റങ്ങളുടെ കാര്യത്തിൽ ഇലക്ട്രോണുകൾ ന്യൂക്ലിയസിനോട് കൂടുതൽ അടുത്തിരിക്കുമെന്നതിനാൽ ഈ എനെർജി കൂടുതൽ ആകണം. പക്ഷേ, ഇവിടെ ഗ്രാഫിൽ കാണിച്ചിരിക്കുന്നതുപോലെയായിരുന്നു കാര്യങ്ങളുടെ കിടപ്പ്.
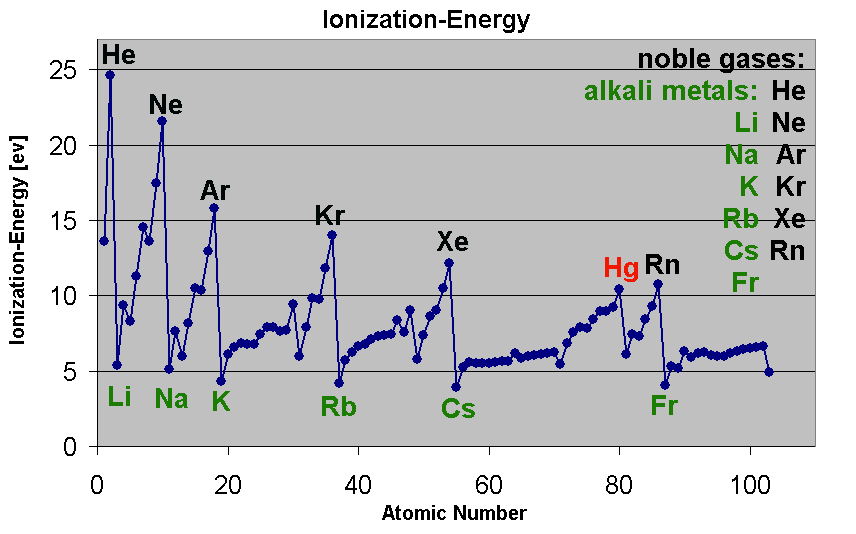
ആവർത്തന പട്ടികയിലെ നോബിൾ വാതകങ്ങളുടെ (He, Ne, Ar,…) കാര്യത്തിൽ അത് താരതമ്യേന ഉയർന്നും ആൽക്കലി ലോഹങ്ങളുടെ (Li, Na, K,…) കാര്യത്തിൽ ഇത് താരതമ്യേന താഴ്ന്നും ഇരിക്കുന്നു. മാത്രവുമല്ല ഇക്കാര്യത്തിൽ ഒറ്റ നോട്ടത്തിൽ തന്നെ ചില പാറ്റേണുകളും കാണാം. ഇതൊക്കെ ബോർ-സമെർഫെൽഡ് മോഡെലിൻ്റെ അടിസ്ഥാനത്തിൽ വിശദീകരിക്കാനുള്ള ശ്രമത്താലാണ് പോളി തൻ്റെ വിഖ്യാത തത്വത്തിൽ എത്തിച്ചേർന്നത്. ആദ്യകാലത്ത് പരിഗണിച്ചത് n, l, m എന്നീ മൂന്നു ക്വാണ്ടം നമ്പറുകളെയായിരുന്നു. ഈ മൂന്നു നമ്പറുകളാൽ രേഖപ്പെടുത്തുന്ന ഒരു ക്വാണ്ടം സ്റ്റേറ്റിൽ പരമാവധി രണ്ടു ഇലക്ട്രോണുകൾ മാത്രമാണ് സാദ്ധ്യമാവുക എന്നതായിരുന്നു ആദ്യകാല പ്രസ്താവന. പിന്നീട് സ്പിൻ എന്നൊരു സംഗതി കൂടി കണ്ടെത്തി. ആദ്യകാലത്ത് പോളിക്ക് അതു സ്വീകാര്യമായി തോന്നിയില്ല. പിന്നീട് അതിൻ്റെ പ്രാധാന്യം തിരിച്ചറിഞ്ഞപ്പോൾ സന്തോഷപൂർവ്വം ഏറ്റെടുത്തു. ഇലക്ട്രോണിൻ്റെ സ്പിൻ ആൻഗുലാർ മൊമെൻ്റത്തിന് ഒരു ദിശയിൽ (+\frac{1}{2}\left(\frac{h}{2\pi}\right)), (-\frac{1}{2}\left(\frac{h}{2\pi}\right)) എന്നിങ്ങനെ രണ്ടു മൂല്യങ്ങൾ എടുക്കാം എന്നും മനസ്സിലായതോടെ സ്പിൻ ക്വാണ്ടം എന്ന മറ്റൊന്നു കൂടി ലിസ്റ്റിൽ ചേർത്തു. അതോടെ ക്വാണ്ടം നമ്പറുകളുടെ എണ്ണം നാലായി. ഈ നാലു നമ്പറുകളും തുല്യമാകുന്ന വിധത്തിൽ രണ്ട് ഇലക്ട്രോണുകൾക്ക് ഒരു ആറ്റത്തിൽ നിലനില്പ് ഇല്ലെന്നതാണ് പോളിയുടെ തത്വം. ഇലക്ട്രോണിൻ്റേതുപോലെയുള്ള സ്പിൻ പ്രോട്ടോൺ, ന്യൂട്രോൺ എന്നിത്യാദി കണങ്ങൾക്കും ഉണ്ടെന്നു പിന്നീട് ബോദ്ധ്യമായി. ഇവയ്ക്കും പോളിയുടെ തത്വം ബാധകമാണ്. ന്യൂക്ലിയസിൻ്റെ ഘടന പഠിക്കുമ്പോൾ ഇതുകൂടി പരിഗണിക്കേണ്ടത് അത്യാവശ്യമാണ്.
6.4 ദി ബ്രോയിയുടെ തരംഗ സിദ്ധാന്തം
ക്വാണ്ടം സയൻസിൻ്റെ ചരിത്രത്തിൽ പ്രധാനപ്പെട്ട ഒരു സംഭവമായിരുന്നു ലൂയി ഡി ബ്രോയ് (Louis de Broglie) എന്ന ഫ്രഞ്ചു ശാസ്ത്രജ്ഞൻ അവതരിപ്പിച്ച തരംഗ സിദ്ധാന്തം. ഇതനുസരിച്ച് പ്രകാശത്തിന് തരംഗസ്വഭാവത്തോടൊപ്പം കണികാസ്വഭാവവും ഉള്ള പോലെ ഇലക്ട്രോൺ പോലുള്ള കണികകൾക്ക് കണികാ സ്വഭാവത്തിനു പുറമേ തരംഗ സ്വഭാവവും ഉണ്ട്.

ഇദ്ദേഹത്തിന്റെ സിദ്ധാന്തം അനുസരിച്ച് (p) മൊമെന്റം ഉള്ള ഒരു കണവുമായി ബന്ധപ്പെട്ട തരംഗത്തിന്റെ തരംഗദൈർഘ്യം,
\begin{equation}
\lambda=\frac{h}{p}
\end{equation}
ഇവിടെ (h) എന്നത് പ്ലാങ്ക് സ്ഥിരാങ്കം ((h=6.6\times 10^{-34} Js). പ്രകാശത്തെ അപേക്ഷിച്ച് വളരെ കുറഞ്ഞ വേഗത്തിൽ പോകുന്ന കണങ്ങളുടെ കാര്യത്തിൽ (p=mv). ഇവിടെ (m) എന്നത് മാസ്, (v) എന്നത് വേഗം. സാമാന്യം വലിയ വേഗത്തിലുള്ള വസ്തുക്കളുടെ കാര്യത്തിൽ (p=\frac{mv}{\sqrt{1-\frac{v^2}{c^2}}}).
ഇദ്ദേഹം പറയുന്ന രീതിയിൽ വസ്തുക്കൾക്ക് തരംഗ സ്വഭാവം ഉണ്ടെങ്കിൽ അത് നമ്മൾ നിത്യജീവിതത്തിൽ കാണാത്തത് എന്തേ ചോദ്യം ന്യായമാണ്. ഒരു ചെറിയ കണക്കുകൂട്ടൽ നടത്തിയാൽ നമുക്ക് അതിൻ്റെ ഉത്തരം കണ്ടെത്താം. ഉദാഹരണമായി ഒരു കിലോഗ്രാം മാസുള്ള ((m=1 kg)) ഒരു വസ്തു (10 m/s) വേഗത്തിൽ സഞ്ചരിക്കുകയാണെങ്കിൽ, തരംഗദൈർഘ്യം എന്നത്
\begin{equation}
\lambda=\frac{h}{mv}=\frac{6.6\times 10^{-34} Js}{1 kg\times 10 m/s}=6.6\times 10^{-35} m
\end{equation}
അതായത്,
\begin{equation}
\lambda= 0.000,000,000,000,000,000,000,000,000,000,000, 066 {\text{മീറ്റർ}}.
\end{equation}
ഇത് ഇത്ര ചെറുത് ആയതിനാൽ നമുക്ക് തിരിച്ചറിയാൻ കഴിയില്ല എന്നത് ഉറപ്പല്ലേ?
അതേ സമയം, വളരെ ചെറിയ കണങ്ങളുടെ കാര്യമെടുക്കുകയാണെങ്കിൽ കഥ മാറും. ഉദാഹരണമായി ഒരു ഇലക്ട്രോണിൻ്റെ കാര്യം പരിഗണിക്കുക. അതിൻ്റെ മാസ് (9.1\times 10^{-31} kg) മാത്രം. ഒരു വോൾട്ട് പൊട്ടെൻഷ്യൽ വ്യത്യാസത്തിലൂടെ കടത്തിവിട്ടാൽ അതിനു ലഭിക്കുന്ന ഊർജം ഒരു ഇലക്ട്രോൺ വോൾട്ട്, അതായത് (1.6\times 10^{-19}) ജൂൾ. ഇത്രയും ഊർജമുണ്ടെങ്കിൽ അതിന് എത്ര മൊമെൻ്റം ഉണ്ടാകുമെന്ന് കണക്കാക്കാൻ നമുക്ക് ഈ സമവാക്യങ്ങൾ ഉപയോഗിക്കാം;
\begin{equation}
E= \frac{1}{2} mv^2=\frac{(mv)^2}{2m}=\frac{p^2}{2m}
\end{equation}
അങ്ങനെയെങ്കിൽ, മൊമെൻ്റം കാണാൻ
\begin{equation}
p^2=2mE\quad\Rightarrow\quad p=\sqrt{2mE}
\end{equation} ഇത്രയും ഉപയോഗിച്ച് നമുക്ക് തരംഗദൈർഘ്യം ((\lambda) കണക്കാക്കാനുള്ള സമവാക്യം ഇങ്ങനെയെഴുതാം;
\begin{equation}
\lambda=\frac{h}{p}=\frac{h}{\sqrt{2mE}}
\end{equation}
ഒരു വോൾട്ട് പൊട്ടെൻഷ്യൽ വ്യത്യാസത്തിലൂടെ കടന്നു പോയ ഒരു ഇലക്ട്രോണിൻ്റെ കാര്യത്തിൽ,
\begin{equation}
\lambda=\frac{h}{\sqrt{2mE}}=\frac{6.6\times 10^{-34} Js}{\sqrt{2\times 9.1\times 10^{-31} kg\times 1.6\times 10^{-31}J}}=
1.2\times 10^{-9}m=1.2\,nm.
\end{equation}
അതായത് 1.2 നാനോമീറ്റർ. പക്ഷേ, ഒരു ഇലക്ട്രോണിൻ്റെ കാര്യത്തിൽ ഇതത്ര ചെറിയ അളവല്ല. നാനോമീറ്റർ എന്നത് ആറ്റങ്ങളുടെയും തന്മാത്രകളുടെയും അളവ് കുറിക്കാൻ പറ്റിയ ഒരു യൂണിറ്റാണ്.
ലൂയി ദി ബ്രോയിക്ക്ഇ ഈ സമവാക്യം എവിടുന്നു കിട്ടി എന്നു ചോദിച്ചാൽ അതിനുള്ള ഒരു ഉത്തരം പ്രകാശത്തിൻ്റെ കാര്യത്തിൽ സമാനമായ സമവാക്യം ഉണ്ടല്ലോ എന്നതാണ്. പ്രകാശത്തിൻ്റെ കാര്യത്തിൽ ഫോട്ടോണുകൾക്ക് (E=h\nu) എന്ന അളവിൽ ഊർജത്തിനു പുറമേ (p=E/c) എന്ന അളവിൽ മൊമെൻ്റവും ഉണ്ടെന്ന് ഐൻസ്റ്റൈൻ കണ്ടെത്തിയിരുന്നു. അതൊക്കെ ചേർത്തുവെച്ചാൽ,
\begin{equation}
\frac{h}{p}=\frac{h}{\left(\frac{E}{c}\right)}=\frac{hc}{E}=\frac{hc}{h\nu}=\frac{c}{\nu}=\lambda
\end{equation}
ഇതു ദ്രവ്യകണങ്ങളുടെ കാര്യത്തിലും ശരിയാണെമെന്ന് ലൂയി ദി ബ്രോയി വാദിച്ചു.
ഇതുകൂടാതെ, മറ്റൊരു കണ്ടെത്തലും ഇതിനു ബലം നൽകി. ഹൈഡ്രജൻ ആറ്റത്തിൻ്റെ കാര്യത്തിൽ ആംഗുലർ മൊമെൻ്റം (L=n\frac{h}{2\pi}) എന്ന സമവാക്യമനുസരിച്ച് നിശ്ചിത മൂല്യങ്ങൾ മാത്രമേ സ്വീകരിക്കൂ എന്ന് നീൽസ് ബോർ ഉറപ്പിച്ചു പറഞ്ഞിരുന്നുവെങ്കിലും അതിന് തക്ക ന്യായീകരണമൊന്നും അദ്ദേഹത്തിൻ്റെ പക്കൽ ഉണ്ടായിരുന്നില്ല. എന്നാൽ ഇക്കാര്യത്തിൽ ഡി ബ്രോയി ഒരു ന്യായം കണ്ടെത്തി. അത് ഇതായിരുന്നു; ഇലക്ട്രോൺ തരംഗങ്ങൾ ആറ്റത്തിൻ്റെ ന്യൂക്ലിയസിനു ചുറ്റും നിലനിൽക്ക ണമെങ്കിൽ ഇലക്ട്രോണിൻ്റെ വൃത്താകാര പഥത്തിൻ്റെ ചുറ്റളവ് (പെരിമീറ്റർ (=2\pi r)) തരംഗദൈർഘ്യത്തിൻ്റെ ഗുണിതങ്ങളായിരിക്കണം. അതായത്,
\begin{equation}
2\pi r=n\lambda
\end{equation}
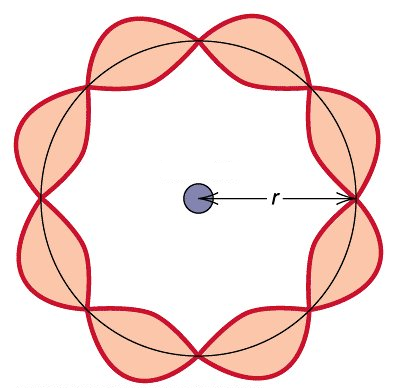
ഈ സമവാക്യത്തിൽ (\lambda) -ക്കു പകരം ഡി ബ്രോയിയുടെ സമവാക്യം അനുസരിച്ച്, (\frac{h}{p}) എന്നു പകരം വച്ചാൽ,
\begin{equation}
2\pi r=n\frac{h}{p}
\end{equation}
ഇതിൽ ചെറിയ തിരിമറികൾ നടത്തിയാൽ
\begin{equation}
p\times 2\pi r=nh
\end{equation} എന്നും അതിൽ നിന്ന് ആംഗുലാർ മൊമെന്റത്തിന്
\begin{equation}
L=pr=\frac{nh}{2\pi}
\end{equation} എന്നും എഴുതാം. ഇതാണല്ലോ നീൽസ് ബോറിനു വേണ്ടിയിരുന്നതും. 1924-25 കാലഘട്ടത്തിലാണ് ഡി ബ്രോയി ഈ ആശയങ്ങൾ പ്രസിദ്ധീകരിച്ചത്. ഐൻസ്റ്റൈൻ, ഷ്രോഡിങ്ഗർ എന്നിങ്ങനെ പലരും ഇതു ഗൗരവത്തിലെടുത്തു. ഇതിൻ്റെ അടിസ്ഥാനത്തിലാണ് വേവ് മെക്കാനിക്സ് നിലവിൽ വരുന്നത്. 1927-28 കാലഘട്ടത്തിൽ നടന്ന ചില പരീക്ഷണങ്ങൾ ഡി ബ്രോയിയുടെ ആശയങ്ങൾക്ക് സംശയരഹിതമായ തെളിവുകൾ നൽകി. അവയെക്കുറിച്ച് നമ്മൾ അടുത്ത സെക്ഷനിൽ ചർച്ച ചെയ്യും. സിദ്ധാന്തങ്ങൾ അവതരിപ്പിച്ചതിനു ശേഷം അധികം വൈകാതെ 1929-ൽ നോബെൽ പുരസ്കാരം നൽകി ശാസ്ത്രലോകം അദ്ദേഹത്തെ ആദരിച്ചു.
6.5 ദ്രവ്യതരംഗങ്ങൾക്ക് പരീക്ഷണങ്ങളുടെ പിന്തുണ


ലൂയി ദി ബ്രോയി ഈ ആശയങ്ങളെക്കുറിച്ചൊക്കെ ആലോചിക്കുന്ന കാലത്തുതന്നെ പലയിടങ്ങളിലും ഇലക്ട്രോണുകളെ ഉപയോഗിച്ച് ചില പ്രധാന പരീക്ഷണങ്ങൾ നടക്കുന്നുണ്ടായിരുന്നു. അതിലൊന്ന് യു.എസ്. എ യിലെ ബെൽ പരീക്ഷണശാലയിൽ ഡേവിസ്സണിൻ്റെ (Clinton Davisson) നേതൃത്വത്തിൽ നടക്കുന്നതായിരുന്നു. 1927-ൽ അദ്ദേഹം പരീക്ഷണങ്ങളിൽ ചില പരിഷ്കാരങ്ങൾ വരുത്തി ദി ബ്രോയിയുടെ സമവാക്യം പരിശോധിക്കാൻ തീരുമാനിച്ചു. സഹായിയായി ജെർമെറും (Lester Germer) ഉണ്ടായിരുന്നു. നല്ല ശൂന്യതയിൽ ഇലക്ട്രോണുകളെ കടത്തിവിട്ട് ഒരു നിക്കൽ കഷണത്തിൻ്റെ പ്രതലത്തിൽ വീഴിക്കുകയായിരുന്നു പരീക്ഷണം. ഇതിനിടയിൽ ഒരു അബദ്ധം പറ്റി. എങ്ങനെയോ വാക്വം ചേമ്പറിലേക്ക് വായു കടന്നു. അതോടെ നിക്കലിൻ്റെ പുറത്ത് നിക്കൽ ഓക്സൈഡിൻ്റെ ഡിപ്പോസിറ്റ് ഉണ്ടായി. അതു നീക്കാനായി നിക്കൽ കഷണത്തെ ഒരു ഓവനിൽ വെച്ച് ഉയർന്ന താപനിലയിൽ സെറ്റ് ചെയ്ത് ചൂടാക്കി. ആ പ്രക്രിയയിൽ മറ്റൊന്നു കൂടി സംഭവിച്ചു, നിക്കലിൽ ക്രിസ്റ്റലീകരണം ഉണ്ടായി. ഇതു വെച്ച് പരീക്ഷണം ആവർത്തിച്ചപ്പോൾ രസകരമായ ഒരു റിസൽട്ട് കിട്ടി. നിക്കലിൽ നിന്ന് തെറിച്ചു വന്ന ഇലക്ട്രോണുകൾ ഒരു ഡിഫ്രാക്ഷൻ പാറ്റേൺ ഉണ്ടാക്കുന്നതായി ഇവർ മനസ്സിലാക്കി. എക്സ്-റേയുടെ കാര്യത്തിൽ ഇതേ പോലെ തന്നെയുള്ള ക്രിസ്റ്റലുകൾ സമാനമായ പാറ്റേൺ ഉണ്ടാക്കുന്ന കാര്യം ശാസ്ത്രജ്ഞർക്ക് അറിവുള്ളതായിരുന്നു. രണ്ടു കാര്യങ്ങളിലും തരംഗ സ്വഭാവമാണ് ഡിഫ്രാക്ഷൻ പാറ്റേൺ ഉണ്ടാക്കുന്നത്.
54 വോൾട്ടിൽ ഇലക്ട്രോണുകളെ ആക്സിലറേറ്റ് ചെയ്താണ് അവർ പരീക്ഷണം നടത്തിയത്. തരംഗദൈർഘ്യത്തിന് അവർക്കു കിട്ടിയ മൂല്യം (\lambda=0.165\, nm). മുകളിൽ കൊടുത്തിരിക്കുന്ന ഫോർമുല വെച്ചു കണക്കാക്കിയപ്പോൾ അവർക്കു കിട്ടിയത് (0.167\, nm). ഇത് ലൂയി ദി ബ്രോയിയുടെ സിദ്ധാന്തത്തിനു ലഭിച്ച വലിയ അംഗീകാരമായി.

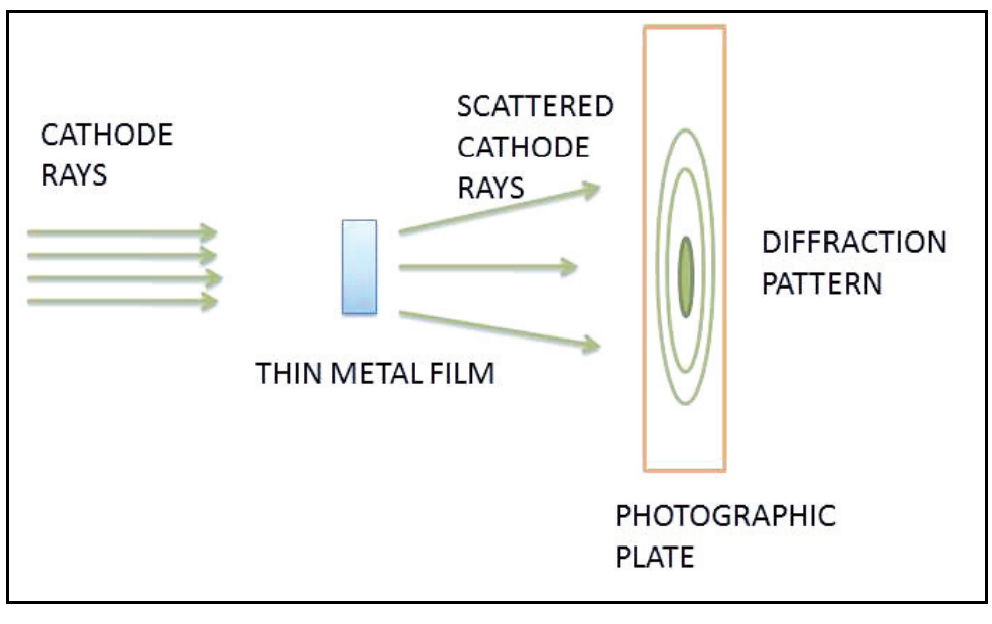
ഏതാണ്ട് ഇതേ സമയത്തു തന്നെ സ്കോട്ട്ലൻഡിൽ ജി.പി. തോംസണും അദ്ദേഹത്തിൻ്റെ ശിഷ്യൻ അലക്സാണ്ടർ റീഡും (Alexander Reid) ഇലക്ട്രോൺ ബീമിനെ ഒരു മില്ലിമീറ്ററിന്റെ ലക്ഷത്തിലൊന്നു ഭാഗം മാത്രം കട്ടിയുള്ള ഷീറ്റിലൂടെ കടത്തിവിട്ട് അതിനു സംഭവിക്കുന്ന ഡിഫ്രാക്ഷൻ പഠിക്കുകയായിരുന്നു. അതിൽ നിന്നു കിട്ടിയ പാറ്റേണുകളും ഇലക്ട്രോണുകളുടെ തരംഗസ്വഭാവം ബോദ്ധ്യപ്പെടുത്തുന്നവയായിരുന്നു. എന്നാൽ, നിർഭാഗ്യകരമെന്നു പറയട്ടെ, പരീക്ഷണ പരമ്പര പൂർത്തിയാക്കും മുമ്പേ ഒരു മോട്ടോർസൈക്കിൾ അപകടത്തിൽ റീഡ്, തൻ്റെ 22-ാം വയസ്സിൽ മരണപ്പെട്ടു.
1937 – ലെ ഫിസിക്സ് നോബെൽ പുരസ്കാരം ഡേവിസണും തോംസണും പങ്കിട്ടു. അതിനിടയിൽ ഒരു കാര്യം എഴുതാൻ വിട്ടുപോയി. ജി. പി. തോംസൺ നോബെൽ പുരസ്കാര ജേതാവായ ജെ.ജെ. തോംസണിൻ്റെ മകനാണ്. പിതാവിന് പുരസ്കാരം ലഭിച്ചത് ഇലക്ട്രോൺ കണമാണെന്നു തെളിയിച്ചതിന് ആണെങ്കിൽ മകന് സമ്മാനം കിട്ടിയത് അത് തരംഗമാണെന്നു തെളിയിച്ചതിനാണ്.

ക്വാണ്ടം കോഴ്സിന്റെ ഭാഗമായി ഇതുവരെ പങ്കിട്ട കുറിപ്പുകൾ
